선형 회귀(Linear Regression) (2) : 모델 성능 평가 1 (평가 지표)

선형 회귀(Linear Regression)

(1) 파라미터 추정

(2) 모델 성능 평가 1 (평가 지표)

(3) 모델 성능 평가 2 (가설 검정)

 

 

들어가기 전에

이 글은 내가 개인적으로 공부한 내용을 기록으로 남기고자 정리한 게시글이기 때문에, 설명이 명확하지 않은 부분이 존재하고 잘못된 내용이 존재할 수도 있어 학습으로서의 가치는 떨어질거라고 본다. 단지 참고만 하자.
그래도 이 글을 읽으실 분들은, 혹시 이 글에서 틀린 부분이 있다면 지적해 주시면 감사하겠습니다..!

 

https://youtu.be/4Yo297HQyAk

참고로 이 파트는 공부할 때 이 영상 (위에 언급한 바로 그 영상입니다.)을 많이 참고했어요. 때문에 필기한 내용을 토대로 적는 이 글의 특성상 영상과 똑같은 설명이 나올 수도 있는데, 만일 이것이 문제가 된다면 댓글로 알려주시면 감사하겠습니다. :-)

 

 

1. 도출된 모델이 얼마나 좋은 모델인지 어떻게 알 수 있을까?

(1)에서 우리는 OLS(최소제곱법)을 통해 선형회귀 모델의 파라미터를 도출하는 법에 대해 알아보았다.

그렇다면, 다음 질문에는 어떻게 답할 수 있을까?

독립변수 $X$, 종속변수 $Y$ 간의 관계를 나타내는 모델1과 $X'$와 $Y'$ 간의 관계를 나타내는 모델2가 있다. 이 두 모델 중 변수 간의 상관관계를 더 잘 나타내는 모델은 무엇인가?

 

여러 방법이 있겠지만 가장 쉽게 직관적으로 와닿는 방법은 아래와 같지 않을까.

"최소제곱법의 정의를 생각해보면, 모델을 평가하는 기준도 $ \sum \text{오차}^2 $와 관련이 있을 거야. $ \sum \text{오차}^2 $와 관련된 수치가 적을 수록 좋은 모델이 아닐까?"

$ \sum \text{오차}^2 $를 그대로 평가 지표로 쓰기에는 무리가 있다. 단순히 오차^2를 더해가기 때문에 n(표본 수)이 클 수록 값이 커지기 때문이다.

그렇기 때문에 이 값에 평균을 취해 사용하는데, 이를 MSE(Mean Squared Error)라고 한다.

 

MSE 외에도 모델을 평가하는 지표는 여러가지가 있다. 차근차근 알아보자.

그 전에 먼저 '자유도'의 개념부터 짚고 넘어갈까 한다.

 

 

2. 자유도(Degree of freedom) 란?

!주의! 이 부분은 통계학도도 아닐 뿐더러 학교에서 통계학을 배운 적이 없는 저에겐 매우 어려운 개념이라 곧곧에 오개념이 존재할 수 있습니다. 다른 자료들과 충분히 교차 검증을 한 뒤 참고하시기 바랍니다.

 

위키피디아의 문서 앞부분에서 필요한 부분만 가져왔다. 사실 읽고 이게 무슨 말이야? 할 수도 있다. 나도 그랬으니까...

 

통계학에서, 자유도는 통계 수치의 마지막 계산 때 자유롭게 버릴 수 있는 값들의 수이다.

자유도는 시스템의 position을 완전히 특정지을 수 있는 독립적인 좌표의 최소 개수로 정의될 수 있다. (??)

모수(statistical parameter) 추정에 쓰이는 정보의 독립적인 piece의 수는 "자유도"라 불린다.

일반적으로 파라미터 추정의 자유도는 다음과 같다.

(추정에 쓰이는 독립변수의 개수) - (해당 파라미터를 추정할 때 intermidiate 단계로서 사용되는 파라미터의 수)

 

intermidiate step이 무슨 말이지... 할 수도 있을 것 같다. 나도 정확한 의미는 잘 모르겠으나 문맥으로 미루어보았을 때, 몇몇 파라미터의 경우 글 (1)에 언급했던 $\widehat{\beta}_0 = \bar{y} - \widehat{\beta}_1\bar{x} $ 처럼 해당 파라미터가 또 다른 parameter

(그런데 사실 모평균이 아닌 표본평균이므로 parameter(모수)보단 statistics(통계량)라고 하는 게 더 맞는 것 같다.)

를 구성 요소로 갖는 것을 볼 수 있는데, 이를 뜻하지 않을까 싶다.

(-> 그리고 이런 통계량을 추정치라고 부르는 것 같다.)

 

즉 저 말을 다시 정리해보자면

(추정에 쓰이는 독립변수의 개수) - (추정치로 사용되는 통계량의 수)

가 된다.

 

 

더 쉬운 이해를 위해 예시를 보자. (이것도 출처는 아까와 동일한 위키피디아 문서)

 

독립 표본 $ X_1, \cdots, X_n $ 이 있다고 하자. 이 변수들은 n차원의 random vector로 나타낼 수 있다.

$  \begin{pmatrix} X_1 \\ \vdots \\ X_n \end{pmatrix}  $   : 이 random vector는 n차원 space의 어디든지 위치할 수 있으므로, n의 자유도를 갖는다.

$ \bar{X} $를 표본 평균이라 하자. 그럼 random vector는 표본 평균 + residual(잔차) vector로 정의될 것이다.

$$  \begin{pmatrix} X_1 \\ \vdots \\ X_n \end{pmatrix} = \bar{X} \begin{pmatrix} 1 \\ \vdots \\ 1 \end{pmatrix} + \begin{pmatrix} X_1 - \bar{X} \\ \vdots \\ X_n - \bar{X} \end{pmatrix} $$

우변의 첫 번째 벡터를 보자. 이는 1 vector의 스칼라곱이다. 즉 자유로운 것은 $ \bar{X} $뿐이므로 1의 자유도를 가진다.

그럼 그 다음 벡터를 보자. 얼핏 보면 n차원의 vector이므로 n의 자유도를 가진다~ 라고 볼 수 있을 것 같지만 아니다.

이 벡터는 자세히 보면 각 변수에서 평균을 뺀 값으로 이루어져 있으므로, 편차들로 이루어져 있다고 볼 수 있다. 그럼 편차의 성질(편차의 합=0)에 의해, 이 벡터도 원소들의 합이 0이 될 것이다.

즉 $ \sum_{i=1}^n \left( X_i - \bar{X} \right) = 0 $ 의 성질을 가진다. 그리고 해당 벡터의 원소들은 이런 성질에 의해 제한을 받는다. 왜냐하면, vector의 앞 n-1개 컴포넌트는 어떤 것이든 될 수 있지만, n-1개가 정해지면 n번째 컴포넌트는 저절로 정해지기 때문이다.

그러므로 이 벡터는 n-1의 자유도를 가진다.

 

그리고 이 결과는 아까 위에서 언급한

(추정에 쓰이는 독립변수의 개수) - (추정치로 사용되는 통계량의 수) = n - 1(평균)

과 동일한 것을 알 수 있다.

 

 

2-1. 여러 통계량의 자유도

들어가기 전에 함수를 하나 정의하고 가겠다. 자유도(degree of freedom)의 앞 철자를 따 df라는 이름의 함수이고, 이름 그대로 여기에 어떤 인자가 들어가면, 해당 인자의 자유도를 반환한다.

• df(표본평균) = n

 

• df(표본표준편차) = n-1

( $ \because s = \sqrt { \frac { \sum_i \left( X_i - \bar{X} \right) ^2 } { n } } $ 이므로 아까의 식에 적용시키면 n(변수의 개수) - 1(평균) )

 

• df(error) = n - (k+1)  (k : slope 개수)

 

df(error)가 왜 저렇게 되냐면

$ error = \left| y - \widehat{y} \right| = \left| y - \left( \beta_0 + \beta_1 x_1 + \cdots \ + \beta_k x_k \right) \right| $ 이고, 회귀 모델 식의 계수(coefficients)들이 전부 다 추정치이다.

그러므로 n에서 추정치의 개수 (k + 1)을 빼 주면 (intercept가 존재하기에 k가 아니라 k+1) error의 자유도가 나온다.

 

여기서 왜!!!! coefficients가 다 추정치죠??? 평균 표준편차 이런 것도 아닌데....? 하는 분들을 위한 나의 뇌피셜

언급된 사람 = 바로 나야나....

직관적으로 이해되는 사람들은 아~ coefficient들이 주어지면 독립변수 n개 중 몇 개가 자동으로 구해지구나~ 하고 넘어가시면 됩니다. (사실 이게 가장 베스트..)

전 머리를 치면 깡 소리가 나는 돌머리이기 때무네... 거기다가 쓸데없이 호기심은 또 왕성... 왜 이렇게 되는지 직접 해보았읍니다.

 

 

우선 단순화를 위해 선형 회귀 모델이 X가 하나밖에 없는, 단순 선형 회귀 모델이라고 가정해보자. 그러면 coefficient는 $ \beta_0, \beta_1 $ 두 개이다. 그리고 이 두 파라미터는 (1)에서 이미 구했다. 식을 다시 떠올려 볼까.

 

$$  \widehat{\beta}_0 = \bar{y} - \widehat{\beta}_1\bar{x}  $$

$$  \widehat{\beta}_1 = \frac {\sum \left( x_i - \bar{x} \right) \left( y_i - \bar{y} \right)} {\sum \left( x_i - \bar{x} \right) \left( x_i - \bar{x} \right)}  $$

 

$\widehat{\beta}_0$를 보자. 이를 구하기 위해서는 $\bar{X}$를 알아야 한다. $\Rightarrow$ 자유도 -1

$\widehat{\beta}_1$을 구하기 위해서는 $\sum \left( x_i - \bar{x} \right)^2$ (편의상 $SS_{xx}$라 하겠음)를 알아야 한다. $\Rightarrow$ 자유도 -1

    proof.) <1> $ x_1 + x_2 + \cdots + x_n = n\bar{x} $

              <2> $ \left( x_1 - \bar{x} \right)^2 + \cdots + \left( x_n - \bar{x} \right)^2 = SS_{xx} $

              $ x_1 $부터 $ x_{n-2} $ 까지는 안다고 가정하면 우리가 구해야 할 값은 $ x_{n-1}, x_n $

              그럼 위의 <1>, <2>식의 대부분이 상수가 되는데 이를 반영하여 다시 쓰면 (\widehat{\beta}_0, \widehat{\beta}_1 이미 아는 상태)

              <1> $ x_{n-1} + x_n = \text{상수} $

              <2> $ \left( x_{n-1} - \bar{x} \right)^2 + \left( x_n - \bar{x} \right)^2 = \text{상수} $

              <1>과 <2>를 연립하면 미지수 $x_{n-1}, x_n$은 쉽게 구할 수 있을 것이다.

              그러므로 $SS_{xx}$를 알면 독립변수를 하나 덜 알아도 되기 때문에 자유도가 -1 깎이는 것.

 

비슷하게 k개의 slope와 1개의 intercept가 주어진 경우 coefficient의 수만큼(k+1)의 독립변수를 덜 알아도 되기 때문에 자유도는 n - (k + 1)이 되는 것이다.

(물론 내 뇌피셜이기 때문에 너무 맹신하지는 말길 바란다.)

 

 

3. SSE, SSR, SST

자유도 다음부터 본격적으로 성능 평가 수치들을 소개하려 했는데, 그 전에 또 용어를 짚고 넘어가야 할 것이 있어 이렇게 칸을 마련했다. (SSE는 이전 문서 (1)에서 언급한 것이기도 하다.)

 

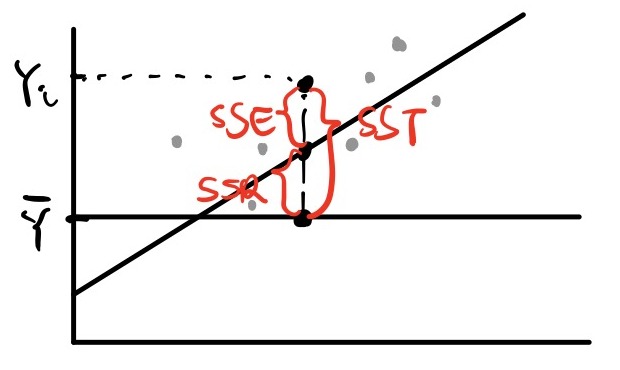
그림이 좀 허접해도 이해 바람...

• SSE (Error Sum of Squares)

에러의 제곱의 합. 여기서 에러는 모델로 예측한 값과 실제 값의 차이를 뜻한다.

$$  SSE = \sum_{i=1}^n \left( Y_i - \widehat{Y}_i \right) ^2  $$

 

• SSR (Regression Sum of Squares)

회귀 모델로 예측한 값과 실제 값의 평균($ \bar{Y} $)의 차의 제곱합

$$ SSR = \sum_{i=1}^n \left( \widehat{Y}_i - \bar{Y} \right) ^2  $$

• SST (Total Sum of Squares)

실제 값과 실제 값의 평균($ \bar{Y} $)의 차의 제곱합

$$  SST = \sum_{i=1}^n \left( Y_i - \bar{Y} \right) ^2  $$

 

SST는 SSR과 SSE의 합으로 표현할 수 있다.

즉 $ SST = SSR + SSE $ 이다.

일반적으로는 통하지 않을 등식이겠지만, 선형 회귀 모델의 경우 최소 제곱법(Least Squares)를 전제로 하고 있기 때문에 식이 성립한다. 자세한 증명이 궁금하다면 여기로.

 

만약 $ \frac {SSR} {SST} =1 $ 이라면, $ SST = SSR $ 이 되어 $ SSE = 0 $ 이 된다.

이는 $ Y = \widehat{Y} $ , 에러가 하나도 없다는 것을 뜻한다.

 

만약 $ \frac {SSR} {SST} =0 $ 이라면, $ SST = 0 \Rightarrow SST = SSE $ 가 된다.

이는 $X$를 사용해 예측값을 도출해도 $\bar{Y}$를 사용한 것에 비해 $Y$를 설명하는 데 도움이 되지 않았다는 것을 뜻한다. 즉 모델을 다시 만들어라..! 라는 말

 

그렇다면 SSE, SSR, SST의 자유도는 어떻게 될까? (증명에서 내 뇌피셜 조금 있음)

 

• $ df (SST) = n-1 $

$\because$  n(독립 변수의 개수, X와 Y는 대응 관계이므로 X의 개수로 대체해도 무방할 것) - 추정치(평균 1개)

 

• $ df (SSR) = 1 $

$\because\ \widehat{y} $는 파라미터가 2개이므로 둘 사이에 제약이 없다면 자유도는 2가 될 것이다.

그런데 아까 전 $\widehat{\beta}_0$를 구한 식이 기억나는가? $\widehat{\beta}_0 = \bar{y} - \widehat{\beta}_1 \bar{x}$.

$\bar{X}$는 이미 주어졌고 SSR의 정의에 의해 $\bar{Y}$는 이미 주어진 상황이므로 $\widehat{\beta}_0, \widehat{\beta}_1$ 중 하나가 정해지면 다른 파라미터도 정해질 것이다. 그래서 자유도는 2가 아닌 1이 된다.

(!뇌피셜 주의! 이 증명을 할 때 X는 이미 주어진 상태라고 가정했는데, 왜냐하면 SSR에서 자유도를 계산할 때의 독립 변수는 X가 아닌 coefficients인 것 같았기 때문이다. 즉, 변수를 보는 시각이 SST와 다른 것 같았다. 때문에 $\bar{x}$도 자연스레 주어지게 된다.)

 

• $ df (SSE) = n-2 $

2-1에서 다루었던 df (error) 와 똑같은 원리이다.

 

 

4. 여러 가지 평가 지표들

4-1. MSE (Mean Squared Error)

$$  MSE = \frac {1} {N} \sum_{i=1}^N \left( Y - \widehat{Y} \right)^2 $$

글의 첫 부분에 언급했던 지표이다. 딥 러닝에서는 손실 함수로 사용되기도 한다.

 

4-2. $ R^2 $ (R-Squared, 결정 계수)

$$  R^2 = 1 - \frac {\sum \left( y - \widehat{y} \right)^2} {\sum \left( y - \bar{y} \right)^2} = 1 - \frac {SSE} {SST} = \frac {SSR} {SST}  $$

SSR / SST = 회귀선에 의해 설명되는 변동 / 전체 변동,

즉 회귀선이 실제 데이터를 얼마나 가깝게 설명하는지를 수치적으로 나타낸 지표이다.

종속변수(Y)에 대한 독립변수(X)의 설명력을 나타내는 지표,

혹은 단순히 $ \bar{Y} $를 사용했을 때 대비 $X$ 정보를 사용함으로써 얻는 성능 향상 정도라고 생각할 수도 있다.

 

3. 에서 언급했던 내용을 다시 보자.

$ \frac {SSR} {SST} = 1 $ 일 때, $ Y = \widehat{Y} $ 즉 에러가 하나도 없다고 했다.

즉, 에러가 하나도 없을 때 $ R^2 = 1 $ 이 된다.

$ \frac {SSR} {SST} =0 $ 일 때는 SSR = 0, 즉 X를 사용함으로써 얻는 성능향상이 없고, 그냥 Y평균을 쓰는 것과 다를 바가 없다고 했다.

즉 회귀 모델이 평균값을 예측하는 모델과 동일할 경우 $ R^2 = 0 $ 이 된다.

 

결론적으로는 $R^2$는 0과 1사이의 범위를 가진다.

$ 0 \le R^2 \le 1 $

※ $ R^2 < 0 $도 가능하기는 하나, 이는 회귀 모델이 평균값을 예측하는 모델보다 성능이 낮은 비정상적인 상황을 의미하므로 범위에서 제외시킨 듯하다.

 

$R^2$이 1에 가까울수록 해당 모델은 설명력이 높으며, 0에 가까울수록 설명력이 낮다. (= X와 Y사이의 관계를 잘 설명해주지 못한다.)

 

※ 번외로 결정 계수를 왜 R이 아닌 $ R^2 $이라고 부르는지에 대해 의문을 갖고 찾아 봤더니, 이는 결정 계수는 피어슨 상관 계수($\rho$)를 제곱한 값이라는 것과 관련이 있는 것 같다... 출처(이것도 단순선형회귀모델에서만 성립된다고 함) 근데 그 이유를 모르겠으므로 나중에 그 이유를 알게 될 때 여기다가 적기..

 

 

4-3. Adjusted $R^2$ (수정된 결정 계수)

결정 계수에는 한계점이 있다. 가령, 종속 변수 $Y$를 설명하기 위해 기존 독립 변수 $X_1$ 외에도 Y에 영향을 주든 주지 않든 상관하지 않고 독립변수 몇 개($X_2, X_3$)를 싹싹 긁어와 모델을 만들었다고 하자. 새로 만들어진 모델은 기존 모델보다는 그래도 높은 설명력을 보일 것이다. 어떤 독립 변수가 단지 Y값들 중 하나에만 영향을 미쳤더라도 이로 인해 Y에 대한 설명력은 더 올라갈 것이기 때문에. 그래서 결정 계수($R^2$)는 독립 변수의 개수가 많아질수록 그 값이 커진다.

하지만 이렇게 되면 종속 변수(Y)를 잘 설명해주지 못하는 독립 변수(X)가 추가되어도 결정 계수의 값이 커지기 때문에, 불필요한 독립 변수들이 추가된 모델이 더 성능을 좋은 모델이라고 판단해버리는 불상사가 일어날 수 있다.

이런 문제를 해결하기 위해 기존 결정 계수를 보정한 값을 사용하는데, 이를 수정된 결정 계수라고 한다.

 

$$  Adjusted\ R^2 = 1 - \frac {\sum \left( y - \widehat{y} \right)^2 / \left( n - k \right)} {\sum \left( y - \bar{y} \right)^2 / \left( n - 1 \right) } = 1 - \frac {n - 1} {n - k} \times \frac {SSE} {SST} \quad \le R^2  $$

(n : data의 수, k : coefficients 수)

 

식을 자세히 보면 분모 SST는 (n-1)로 나누어 주고, 분자 SSE는 (n-k)로 나누어 준다. 그리고 이 수들은 각각 SST, SSE의 자유도이다. 즉 기존 $R^2$ 식에서 분모, 분자에 해당하는 통계량의 자유도로 각각 나누어 준 것이다.

 

이렇게 하면 값이 보정되어, 독립 변수의 개수가 다른 회귀 모형들의 설명력을 비교할 수 있게 된다.

 

 

4-4. SE (Standard Error of Estimate, 추정 표준 오차)

강의 자료에는 짤막하게 standard error of estimate라고 나와 있을 뿐이고, 구글링을 해도 잘 나오지 않아 한글 명칭이 무엇인지 알 수 없었다. 그래서 그냥 '추정 표준 오차'라고 대충 해석해서 적었다. (해당 용어를 사용하는 곳이 하나 더 있기도 했고..)

 

(단순선형회귀의 경우)

$$  SE = \sqrt { \frac { \sum \left( \widehat{y} - y \right) ^2 } {n - 2} } = \sigma_Y \sqrt { \left( 1 - \rho^2 \right) }  $$

 

실제 값이 회귀선 위의 예측값($\widehat{y}$)으로부터 얼마나 차이나는지 측정하는 지표이다.

두 번째 식에 주목하자. 분자에 SSE가 들어간다. 그리고 분모는 n-2, 즉 SSE의 자유도로 나누어주었음을 알 수 있다. 다중 선형 회귀라면 분모가 달라질 것이다.

 

에러($\epsilon_i = Y_i - \widehat{Y}_i $)이 정규 분포를 따를 때, 그 분포의 표본표준편차 값이기도 하다.

즉, $ \epsilon_i \sim N \left( 0, \sigma_e^2 \right) ,\quad \widehat{\sigma}_e = SE $

(SE 식을 자세히 보면 평균이 0일 때의 표본 표준편차 구하는 식과 동일하다.)

 

SE값은 SSE와 비례하므로, 당연히 값이 작을 수록 좋다.

 

 

4-5. SE of Coefficients (기울기의 표준 오차)

각 coefficient에 대한 표준 오차.

추정한 각 coefficient를 얼마나 정확히 예측했는지 알려 주는 지표이다.

다음 글에 나올 예정인 T-test에서 사용된다. (각 coefficient가 정규 분포를 따를 때, t-통계량을 구하기 위해 표본표준편차 대신 사용된다.)

 

• SE of Slope

$$  SE \left( \beta_1 \right) = \frac {SE} {S_{xx}} = \sqrt{ \frac {\sum \left( \widehat{y} - y \right) ^2 } { \left( n-2 \right) \sum \left( x - \bar{x} \right) ^2 } }  $$

 

이 때 $S_{xx} = \sqrt {SS_{xx}} = \sqrt { \sum \left( x - \bar{x} \right) ^2 } $ 이다.

(이런 용어가 실제로 쓰일진 모르겠는데 강의 자료엔 이렇게 돼 있었다..)

 

• SE of Intercept

$$  SE \left( \beta_0 \right) = SE \times \sqrt { \frac {1} {n} + \frac {\bar{x}^2} {SS_{xx}} }  $$

 

 

부록. 4-5 증명

왜 값이 저렇게 되지? 하는 나같은 분들을 위한 증명

(원래 더보기에 썼는데 그랬더니 LaTex 수식 일부가 먹히지 않는 경우가 발생했다. 그래서 그냥 항목을 따로 빼서 쓴다.)

 

$\widehat{\beta}$의 분산($Var(\widehat{\beta})$)을 구하는 것부터 시작한다.

($\beta$에 ^이 있다고 표본분산이라고 헷갈릴 수 있는데, 아니다. $\beta$에 대한 점추정 $\widehat{\beta}$의 모분산을 구하는 것이다. 그러면 여기서 모분산을 어떻게 구해..? 라고 물을 수도 있을 텐데, 일단은 넘어가자.)

 

$ \widehat{\beta} = \left( X^T X \right) ^{-1} X^T y $ 이기 때문에, $Var(\widehat{\beta})$는 다음과 같다.

(증명)

$$ Var \left[ \widehat{\beta} \right] = Var \left[ \left( X^TX \right) X^Ty \right]  $$

이 때 $y$는 실제 y값이다. 여기서 $y$를 $\epsilon$에 대한 식으로 바꾸어 주자.

$ \epsilon = Y - \widehat{Y} $ 이므로, $ Y = \widehat{Y} + \epsilon $ 을 해당 위치에 넣어 주면,

$$ = Var \left[ \left( X^TX \right) X^T \left( X\widehat{\beta}+\epsilon \right) \right] = Var \left[ \left( X^TX \right)^{-1} X^TX\widehat{\beta} + \left( X^TX \right)^{-1} X^T \epsilon \right]  $$

이 된다. $ \left( X^TX \right)^{-1} X^T = I$ 이므로 결국 식은 다음과 같이 된다.

$$ = Var \left[ \widehat{\beta} + \left( X^TX \right)^{-1} X^T \epsilon \right] $$

분산의 성질에 의해 $ Var(a + X) = Var(X) $ 이므로,

이 식은 옆의 $\widehat{\beta}$가 사라지고 $ Var \left[ \left(X^T X \right)^{-1} X^T \epsilon \right] $ 가 된다.

(이 때 a는 vector. 증명 - 여기의 Addition to constant vectors 파트)

 

분산의 또다른 성질에 의해 $  Var(AX) = A Var \left( X \right) A^T $ 이므로 이에 따라 식을 계산하면 다음과 같다.

(증명 - 이 문서의 Multiplication by constant matrices 파트)

$$  = \left(X^T X \right)^{-1} X^T Var \left[ \epsilon \right] X \left( X^TX \right)^{-1}  $$

$ Var[\epsilon] = \sigma^2 $이므로, 상수 $ \sigma^2 $만 앞으로 빼내면

$$ = \sigma^2 \left(X^TX \right)^{-1} X^TX \left(X^TX \right)^{-1} $$

이 된다. 이렇게 되면 가운데 부분이 $ A^{-1}A $ 꼴로 항등 행렬($I$)이 되어 사라지게 된다. 식을 정리하면 다음과 같다.

$$ \therefore\ Var \left[ \widehat{\beta} \right] = \sigma^2 \left( X^TX \right)^{-1} $$

 

그러나 짐작했듯이 실제 $ Var \left[ \epsilon \right] = \sigma$을 구하는 것은 불가능하다. 왜냐하면 우리는 모든 $\epsilon$을 관찰할 수 없기 때문이다. 그렇기에 $ \sigma $대신 $\epsilon$의 표본표준편차 $\widehat{\sigma}$를 사용해야 한다. 그러려면 애초에 $ Var \left[ \widehat{\beta} \right] $ 가 아닌 $ \widehat{Var} \left[ \widehat{\beta} \right] $ 를 구해야 한다. 그리고 이것이 SE(표준 오차)를 담고 있는 행렬이 된다. (내 뇌피셜이지만 이렇기 때문에 기울기의 '표준 편차'가 아닌 '표준 오차'라고 부르는 듯 하다.)

$$ \therefore\ \widehat{Var} \left[ \widehat{\beta} \right] = \widehat{\sigma}^2 \left( X^TX \right)^{-1} $$

 

$ \widehat{\beta} = \begin{pmatrix} \widehat{\beta}_0 \\ \widehat{\beta}_1 \end{pmatrix} $ 이므로 공분산행렬(covariance matrix) $ Var \left[ \widehat{\beta} \right] $는 다음과 같은 2X2 행렬 구조를 갖는다.

 

$$ Var \left[ \widehat{\beta} \right] = E \begin{bmatrix} \left( \widehat{\beta}_0 - E \left[ \widehat{\beta}_0 \right] \right) \left( \widehat{\beta}_0 - E \left[ \widehat{\beta}_0 \right] \right)  &  \left( \widehat{\beta}_0 - E \left[ \widehat{\beta}_0 \right] \right) \left( \widehat{\beta}_1 - E \left[ \widehat{\beta}_1 \right] \right)  \\  \left( \widehat{\beta}_0 - E \left[ \widehat{\beta}_0 \right] \right) \left( \widehat{\beta}_1 - E \left[ \widehat{\beta}_1 \right] \right)  &  \left( \widehat{\beta}_1 - E \left[ \widehat{\beta}_1 \right] \right) \left( \widehat{\beta}_1 - E \left[ \widehat{\beta}_1 \right] \right) \end{bmatrix}  $$

 

이 때 1행 1열에 해당하는 부분이 (SE of intercept)^2, 2형 2열에 해당하는 부분이 (SE of slope)^2이다. 이 두 식들은 어김없는 분산의 형태를 띄고 있으므로 SE of coefficient를 coefficient 대한 표준 편차라고 봐도 무방하지 않을까 싶다.

어쨌든, 이 위치에 있는 원소들이 무엇인지 알아내서 루트를 취해주기만 한다면 각 coefficient의 SE를 알 수 있을 것이다..!!!

 

아까 전 구한 식 $ Var \left[ \widehat{\beta} \right] = \widehat{\sigma}^2 \left( X^TX \right)^{-1} $를 다시 가져와보자. 우변의 식을 풀면 해당 위치의 원소를 알 수 있을 것이다.

$ X = \begin{pmatrix} 1 & x_1 \\ 1 & x_2 \\ \vdots \\ 1 & x_n \end{pmatrix} $ 이므로, $ X^TX = \begin{bmatrix} n & \sum_{i=1}^n x_i \\ \sum_{i=1}^n x_i & \sum_{i=1}^n x_i^2 \end{bmatrix} $

$$ \Rightarrow\ \left( X^T X \right)^{-1} = \frac {1} {n \sum x_i^2 - \left( \sum x_i \right)^2} \begin{bmatrix} \sum_{i=1}^n x_i^2 & -\sum_{i=1}^n x_i \\ -\sum_{i=1}^n x_i & n \end{bmatrix} $$

$$ \therefore\ Var \left[ \widehat{\beta} \right] = \frac {\widehat{\sigma}^2} {n \sum x_i^2 - \left( \sum x_i \right)^2} \begin{bmatrix} \sum_{i=1}^n x_i^2 & -\sum_{i=1}^n x_i \\ -\sum_{i=1}^n x_i & n \end{bmatrix} $$

 

 

SE of Slope 구하기

 

아까 전 2행 2열이 (SE of Slope)^2라고 했다. 그 부분만 따로 떼서 정리를 해 주자.
$$  SE \left( \widehat{\beta}_1 \right) = \sqrt { \left[ Var \left( \widehat{\beta} \right) \right]_{22} } = \sqrt { \frac {n\widehat{\sigma}^2} {n \sum x_i^2 - \left( \sum x_i \right)^2 } }  $$
이 때 분모는 다음과 같이 나타낼 수 있다.
$$ n^2 \left\{ \frac {\sum x_i^2} {n} - \left( \frac {\sum x_i} {n} \right)^2 \right\} = n^2 \left\{ E \left[ X^2 \right] - \left( E \left[ X \right] \right)^2 \right\} $$
오른쪽 식의 중괄호 안에 있는 것은 분산이다. 그러므로 다음과 같이 바꿀 수 있다.
$$ = n^2 \frac { \sum \left( x_i - \bar{x} \right)^2 } {n} = n \sum \left( x_i - \bar{x} \right)^2  $$
분모에 이를 넣고 $SE \left( \widehat{\beta}_1 \right) $ 식을 다시 고쳐 쓰자.
$$ \therefore\ SE \left( \widehat{\beta}_1 \right) = \sqrt { \frac {n\widehat{\sigma}^2} {n \sum \left(x_i - \bar{x} \right)^2 } } = \frac {\widehat{\sigma}} {S_{xx}} = \frac {SE} {S_{xx}} = \sqrt{ \frac {\sum \left( \widehat{y} - y \right) ^2 } { \left( n-2 \right) \sum \left( x - \bar{x} \right) ^2 } }  $$

 

 

SE of Intercept 구하기

 

아까 전 공분산행렬에서, 1행 1열이 (SE of Intercept)^2라고 했으므로, 그 부분만 따로 가져와 정리해 주자.
$$  SE \left( \widehat{\beta}_0 \right) = \sqrt { \left[ Var \left( \widehat{\beta} \right) \right]_{11} } =\sqrt { \frac {\widehat{\sigma}^2 \sum x_i^2} { n \sum x_i^2 - \left( \sum x_i \right)^2 } }  $$
아까 위에서 했던 것처럼 분모를 $ n \sum \left( x_i - \bar{x} \right)^2 $로 바꾸고, $ \widehat{\sigma}^2$ 를 루트 밖으로 빼낸다. 그 후 분자에 $ \frac { \left( \sum x_i \right)^2 {n} } {n} $ 을 더하고 빼준다.
$$ = \widehat{\sigma} \sqrt { \frac { \sum x_i^2 - \frac { \left( \sum x_i \right)^2 {n} } {n} + \frac { \left( \sum x_i \right)^2 {n} } {n} } { n \sum \left(x_i - \bar{x} \right)^2 } }  $$
분모의 $ n $과 분자의 앞 두 항을 묶으면 분산이 된다. $ SS_{xx} = \sum \left( x_i - \bar{x} \right)^2 $ 라 하면 $ Var = \frac {SS_{xx}} {n} $ 이므로 식은 다음과 같다.
$$ = \widehat{\sigma} \sqrt { \frac {SS_{xx}} {nSS_{xx}} + \frac { \frac { \left( \sum x_i \right)^2 } {n} } {nSS_{xx}} } = \widehat{\sigma} \sqrt { \frac {1} {n} + \frac {\bar{x}^2} {SS_{xx}} } = SE \sqrt { \frac {1} {n} + \frac {\bar{x}^2} {SS_{xx}} }  $$

 

 

 

 

 

오탈자, 혹은 잘못된 내용이 있을 경우 댓글로 제보해 주시면 감사하겠습니다.

 

SE of Coefficients 증명하는 게 가장 힘들었다,,,^^ 역시 호기심이 문제야.... 보통 사람들이 아 그렇군! 하고 넘어가는 걸 나는 못 넘어가서 외국 사이트들 다 뒤지고 다녔다... 덕분에 공부 시간도 늘어남.. 뭐 좋은 거겠지.

다음 글은 그 유명한(?) 가설 검정에 대해 다뤄볼까 한다~!