선형 회귀 (Linear Regression) : (3) 모델 성능 평가 2 (가설 검정)

선형 회귀(Linear Regression)

(1) 파라미터 추정

(2) 모델 성능 평가 1 (평가 지표)

(3) 모델 성능 평가 2 (가설 검정)

(4) 모델 성능 평가 3 (분산 분석, ANOVA) ---> 개인적인 사정으로 내년 초에 작성할 예정 ㅠ_ㅠ

 

들어가기 전에

통계학을 제대로 배우고 이 글을 다시 다듬도록 하겠습니다...
지금 보니 조금 엉망인 부분이 많네요ㅠㅠ
참고만 해주시고, 학습으로서의 가치는 떨어집니다.

 

 

0. 선형 회귀 모델 성능 평가 (결과 검증)

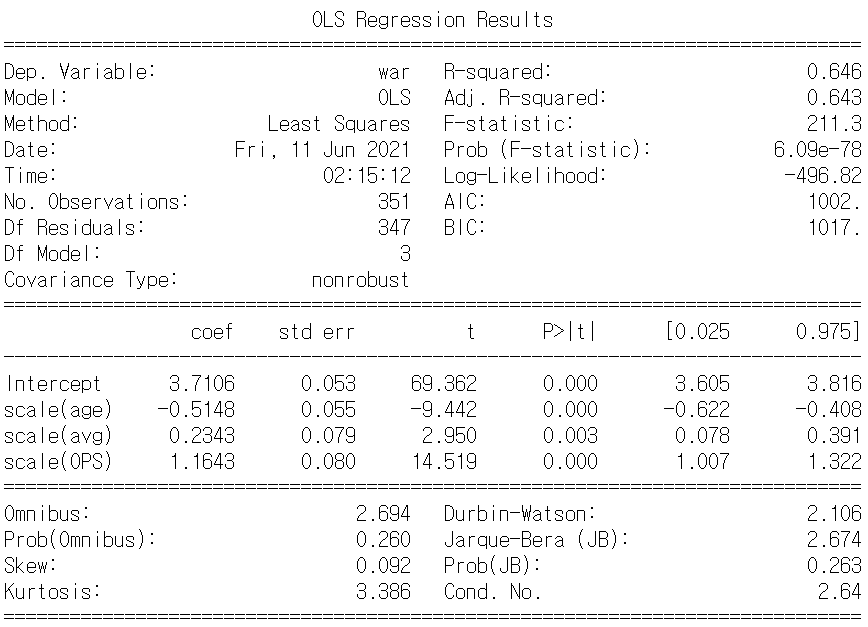
여러 추정 모델들을 제공해주는 statsmodels 라이브러리를 사용하여 OLS 분석을 수행한 결과

선형 회귀를 수행하는 방법엔 여러 가지가 있지만, statsmodels을 사용하면 통계적 검정 결과까지 확인할 수 있다. (2)에서 나왔던 익숙한 이름들도 보일 것이다. 위에서부터 차례대로 내려가며 각 항목이 어떤 건지 알아보자.

 

• No. Observations : 데이터 sample의 수 (n)
• Df Residuals : 잔차($ y - \widehat{y}$)의 자유도. 여기선 독립 변수가 3개이므로 (n - 4) 개
• Df Model : 모델의 자유도. 파라미터 수 4에서 1을 뺀 3이다.
• R-Squared : 결정 계수 ($R^2$)
• Adj, R-Squared : 수정된 결정 계수
• F-statistic : F-통계량 (다음 글에서 서술 예정)
• Prob(F-statistic) : F-통계량을 이용했을 때 얻는 확률 (다음 글에서 서술 예정)
• coef : coefficient. 파라미터 추정 값
• std err : standard error of coefficients
• t : t-statistic (혹은 t-value) (이 글에서 서술 예정)
• p > |t| : p-value (이 글에서 서술 예정)
• [0.025 0.975] : 95%의 신뢰도 구간 (이 글에서 서술 예정)

 

(이 다음으로는 나도 잘 몰라서 설명을 생략한다. 주변에 통계학과 학생이 있으면 그들에게 물어보자.... 난 아무 것도 배운 게 없는 한낱 컴공생이라...)

 

T-test니, t 값, p 값이니 이런 것들을 꽤 많이 들어봤을 것이다.

글 (2)에서 나온 수치들($R^2$, SE 등)은 linear Regression이 어느 정도로 알맞게 되었는가?를 말해 준다면 이 값들은 linear regression이 통계적으로 유의미한지 알려 주는 값들이다.

이 글에서는 이들이 언제 쓰이고 어떻게 도출되는지 알아보고자 한다. 이 글을 읽으면 위의 볼드체 수치들이 무엇을 뜻하는지 이해가 갈 것이다!

 

 

1. 점 추정? 구간 추정?

우리는 선형 회귀 (1) 글에서 파라미터 $ \beta_0, \beta_1 $를 추정했다. 그 때도 언급을 한 번 했었는데, 이것은 파라미터에 대한 점 추정이다. 그런데 추정에는 점 추정 말고 구간 추정이라는 것도 있다. 구간 추정은, 특정 값을 콕 집어 말하는 점 추정과는, 달리 원하는 값이 특정한 구간 사이에 존재한다고 추정하는 것이다.

 

구간 추정의 사례 중 하나로 우리에게 너무 익숙한 모평균 추정이 있을 것이다. (고등학생 때 확통 배우던 기억이 새록새록.)

 

 

1-1. 모평균 추정

모집단의 표준편차($\sigma$)를 알 경우

모집단의 표준편차를 안다고 가정할 때, 중심 극한 정리에 의해 표본 평균은 평균이 모평균이고 표준 편차가 모표준편차/√n인 정규 분포를 따른다.

$$ \bar{X} \sim N \left(\mu, \frac {\sigma^2} {n} \right) $$

알고 싶은 것은 모평균 $\mu$ 이다. 하지만 이것이 무엇인지는 정확히 알 수 없고, 단지 추정을 해야 할 뿐이다.

 

이 그림은 유의 수준을 설명할 때 한 번 더 등장할 예정

신뢰 수준(신뢰도)이 (1-$\alpha$)*100%일 때, 모평균($\mu$)의 신뢰 구간은 다음과 같다.

$$  \bar{X} - z_{\frac{\alpha}{2}} \frac {\sigma}{\sqrt{n}}\ \le\ \mu\ \le\ \bar{X} + z_{\frac{\alpha}{2}} \frac {\sigma}{\sqrt{n}}  $$

이 때 $Z_{\frac{\alpha}{2}}$는 표준정규분포에서 $ P \left( -z \le X \le z \right) = 1-\alpha $ 일 때, 그 때의 Z값이다.

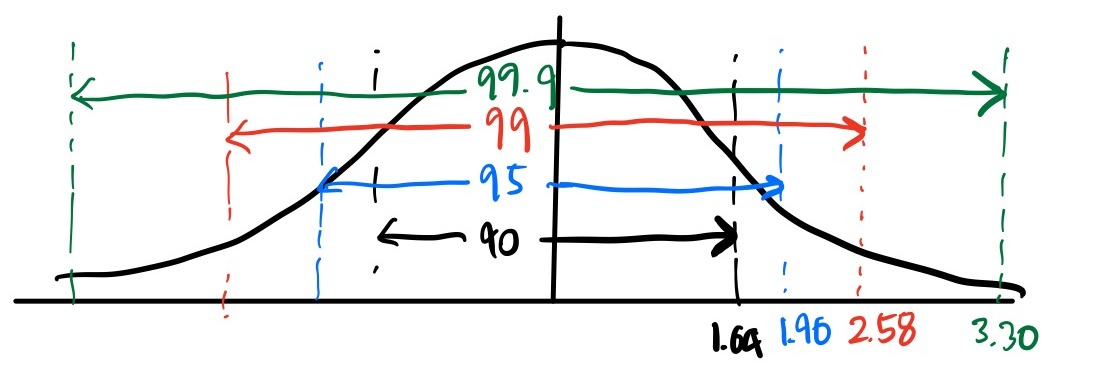
표준정규분포에서 각 신뢰구간 별 신뢰 수준과 그에 해당하는 Z값

저 신뢰 구간 식은 어떻게 해서 나왔는가? 

기존 $\bar{X}$를 표준정규분포에 적용하기 위해 표준화 시킨 후,

$$  Z = \frac { \bar{X} - \mu } { \frac {\sigma} {\sqrt{n}} } $$

이를 $  -z_{ \frac {\alpha}{2}} \le Z \le z_{ \frac {\alpha}{2}} $의 Z에 넣어주면 유도할 수 있다.

 

예시를 들어 더 자세히 구해보자.

(여기서부터 삽질과 뇌피셜이 조금 첨가되어 있으니 어떻게 삽질하는지 궁금하지 않으면 바로 2.로 넘어가기를 추천한다. 2부터는 드디어 가설 검정을 다루기 시작한다.)

우선 편의를 위해 $\alpha=0.05$라 두겠다. 즉 95%의 신뢰 구간에 대해서 말하겠다는 것.

위의 정규 분포 그림에서 가장 중앙은 평균의 위치이다.

여기서는 표본 평균에 대한 분포이므로, 평균은 모평균이 된다. 각 값 하나하나는 표본 평균이 된다.

 

우리에겐 95% 신뢰 수준의 신뢰 구간이 필요하다. 하지만 모평균에 대한 식은 처음부터 구할 수 없으므로 대신 표본평균에 대한 식 $  -z_{ \frac {\alpha}{2}} \le Z \le z_{ \frac {\alpha}{2}} $ 을 사용한다.

$$ P\left(-1.96<z\left(\bar{x}_1\right)<1.96\right) = 0.95 $$

이를 길게 풀어쓰면 다음과 같다.

"모평균이 $\mu$인 모집단에서 표본을 추출하여 표본 평균 $\bar{x}_1$을 구했을 때, 그 값이 '모평균 추정 구간' 안에 속할 확률 = 0.95"    (1)

(실질적으로는 표본 평균의 집단에서 값을 하나 채택한 것이지만, 위와 같이 써도 의미가 동일함)

 

당신이 n개의 표본을 여러 번 추출해서 여러 개의 표본 평균 $\bar{x}_1$, $\bar{x}_2$, $\bar{x}_3$을 구했다고 하자. 이들 또한 95%의 확률로 '모평균 추정 구간'에 들어간다.

즉, 샘플링을 100번 시도하여 표본 평균을 100개 구하면, 그 중 대략 95개 정도는 '모평균 추정 구간'에 들어간다는 것이다.

 

방금 그 식 ($  -z_{ \frac {\alpha}{2}} \le \frac { \bar{X} - \mu } { \frac {\sigma} {\sqrt{n}} } \le z_{ \frac {\alpha}{2}} $) 을 $\mu$에 대한 부등식으로 정리하면, 표본 평균을 기준으로 모평균의 범위를 나타낼 수 있다.

$$  P\left( \bar{X} - 1.96 \frac {\sigma}{\sqrt{n}}\ \le\ \mu\ \le\ \bar{X} + 1.96 \frac {\sigma}{\sqrt{n}} \right) = 0.95 \quad \left(A\right)$$

 

5차례 표본 추출 후 나온 5가지의 신뢰 구간

이 때 중요한 것은 $\mu$ 뿐만 아니라 $\bar{X}$도 고정된 것이 아니라는 것이다.

즉, 신뢰 구간은 고정되지 않는다. 내가 구한 표본 평균 ($\bar{X}$)에 따라 변하는 것이다.

 

확률식A가 무엇을 뜻하는지 길게 풀어 써보자. 단순히 생각하면 식 A는 처음 식을 단순히 모평균에 대해 바꿔주었을 뿐이므로, 설명 (1)을 살짝 바꿔주기만 하면 된다고 생각할지도 모른다.

"모평균의 범위가 이와 같을 경우, 표본 평균이 '모평균 추정 구간'에 들어갈 확률 = 0.95"    (2)

그러나 확률식 A을 잘 살펴보면, 설명 (1)의 바리에이션보다 훨씬 쉽고 직관적인, 새로운 의미를 가지고 있음을 알 수 있다.

"모평균이 이 범위 안에 들어가 있을 확률 = 0.95"

 

사실 '모평균 추정 구간'이 어떤 의미를 뜻하는지 정말 오랜 시간 머리를 감싸고 고민해보고 자료도 많이 찾아 봤는데 쉽사리 답이 나오지 않았다. 결국 내 마음대로 내린 결론은, '단순히 95%의 신뢰수준(확률)을 가지기 위해 이용된 부분이 아닐까.' 이다. 일종의 맥거핀 같은 역할인거지. 아니, 어쩌면 그림 그릴때 잡는 구도 스케치의 역할이 더 어울릴지도 모른다. 95%의 값을 얻기 위해 사용하고, 나중엔 지워버리는. 뭐 이 부분은 깊게 파고든다고 크게 이득이 되는 부분도 없으니 일단은 이렇게만 생각하고 넘어가겠다.

 

그렇다면 이 신뢰수준 95%의 의미는 무엇일까? 이는 아까 언급했던 신뢰 구간 확률식을 보면 쉽게 파악할 수 있다.

$$  P\left( \bar{X} - 1.96 \frac {\sigma}{\sqrt{n}}\ \le\ \mu\ \le\ \bar{X} + 1.96 \frac {\sigma}{\sqrt{n}} \right) = 0.95 $$

조금 전 $\bar{X}$는 고정된 것이 아니라고 했다. 그리고 $\mu$에 대한 부등식이라고 해서, $\bar{X}$에 대한 분포이기에 확률 식 자체는 $\bar{X}$에 대한 식이라는 것을 잊지 않기를 바란다.

 

P = 0.95의 의미는 다음과 같다.

표본 추출을 계속 수행하여 표본 평균($\bar{X}$)을 100개 정도 구하면, 덩달아 신뢰 구간도 구해질 것이다. 이렇게 구해진 신뢰구간 100개 중 대략 95개 정도가 모평균을 포함하고 있다.

 

 

모집단의 표준편차를 모를 경우

이 경우가 현실에 더 가깝다. 모표준편차를 알 가능성은 희박하니까.

이 때는 정규 분포(Z분포)가 아닌 t 분포를 사용한다.

z분포와 t분포를 비교하면 다음과 같다.

$$ Z = \frac { \bar{X} - \mu } { \frac {\sigma} {\sqrt{n}} }, \quad t_{n-1} = \frac {X - \mu} {\frac{s}{\sqrt{n}}}  $$

(이 때 n-1은 자유도)

모표준편차($\sigma$)를 쓰는 Z분포와 달리, t분포는 표본표준편차(s)를 사용하기 때문에 모분산을 몰라도 모평균 추정이 가능하다.

물론 표본의 수 n이 충분히 크면 t분포가 정규 분포에 수렴한다고는 한다.

(t분포에 대한 자세한 설명은 구글 검색 추천..)

 

 

2. 가설 검정과 t-Test

통계적 가설 검정(統計的假說檢定, 영어: statistical hypothesis test)은 통계적 추론의 하나로서, 모집단 실제의 값이 얼마가 된다는 주장과 관련해, 표본의 정보를 사용해서 가설의 합당성 여부를 판정하는 과정을 의미한다.

(출처 위키백과 - 여기도 책의 내용을 인용한 거긴 하지만..)

즉, 가설을 세운 후 표본의 값을 가지고 계산을 하여 해당 가설이 맞는지 틀린지 검증하는 과정이다.

 

가설 검정의 절차는 다음과 같다. 역시 이것도 출처는 위키백과와 이 영상.

1. 가설 수립, 유의 수준($\alpha$) 설정

2. 표본 추출과 검정 통계량 설정

3. 기각역 설정

4. 통계량 계산

5. 의사 결정

 

t-Test(혹은 Student t-Test)는 가설 검정의 대표적인 방법 중 하나이다. 검정 통계량이 귀무 가설 하에서 t 분포를 따른다고 하여 t-테스트라는 이름이 붙게 되었다.

 

그렇다면 t-Test를 각 단계를 거쳐가며 수행하면서 가설 검정이 어떻게 이루어지는지, t-Test는 어떤 것인지 알아보도록 하자.

 

※ 이 문서에 쓰인 t-Test는 '대응 표본 t 검정'이다. t 검정을 치면 일반적으로 나오는 t 검정은 서로 다른 두 모집단에서 데이터를 추출한 뒤 그들 간 평균 차이가 있는지 검정하는 기법이다. 자세한 사항은 이 문서 참조

 

 

2-1. 가설 수립과 유의 수준($\alpha$, significance level) 설정

가설 수립

가설 검정에서 사용되는 가설은 귀무 가설과 대립 가설이 있다.

• 귀무 가설($H_0$) : 연구를 할 필요가 없는 내용의 가설, 혹은 처음부터 버릴 것을 예상하는 가설. 영 가설이라고도 불린다.
• 대립 가설($H_1$) : 연구를 할 필요가 있는 가설.

가설 검정을 수행하면서 두 가설 중 어떤 것을 채택할지 결정하게 된다. 처음에 귀무 가설을 참이라고 두고, 이를 기각할지 말지 판단하는 방식이다. 그렇게 때문에 보통은 자신이 증명하고자 하는 것을 대립 가설로 두고, 그 반대를 귀무 가설로 둔다. (처음에 반대되는 내용을 참이라고 가정하는 이 방법은, 귀류법을 떠올리게 한다. 물론 내 개인적인 생각)

 

 

유의 수준 (significance level)

유의 수준이란, 앞서 언급한 두 가설 중 어느 것이 맞는지 결정하는 기준이 되는 값(확률)이다.

모수를 추정할 때는 항상 오류 가능성을 확률로 제시하는데 그 때 유의수준이 사용된다.

그림을 보면, $ \pm z_{\frac{\alpha}{2}} $를 경계로 해당 경계의 바깥쪽 ($\pm \infty$까지) 부분의 면적의 합은 $\alpha$이고, 안쪽의 면적은 $1-\alpha$이다.

가설 검정에서 검정 통계량(일단은 어떤 값이라고만 이해하자)이 기준값(여기서는 $ \pm z_{\frac{\alpha}{2}} $) 밖에 위치하면 귀무 가설을 기각하고, 안쪽에 위치하면 귀무 가설을 채택하는데, 이 기준값을 결정하는 것이 유의 수준이다. 유의 수준의 값으로는 주로 0.05를 사용하고, 가끔 0.01 등을 사용하는 경우도 있다. 만약 유의 수준이 0.05라면, 기준값 바깥쪽의 면적의 합이 0.05, 안쪽의 면적의 합이 0.95가 된다.

 

다른 말로는 1종 오류를 범할 확률의 최대 크기 (출처) 라고도 한다. 1종 오류와 2종 오류는 이 글에서 따로 설명하지는 않겠다. 구글 검색 추천.

 

다음 파트에서는 검정 통계량이 무엇인지 알아보고자 한다,

 

 

2-2. 검정 통계량($\supset$ t-statistic or t-value)

아까 전 t-Test의 정의에서, '검정 통계량이 귀무 가설 하에서 t 분포를 따른다'고 하였다. 여기서 언급된 '검정 통계량'이 무엇인지 알아보자.

 

검정 통계량이란, 귀무 가설이 참이라는 가정 아래 얻은 통계량(statistics, 표본들의 함수)이다. 추정값(표본평균 등)을 이 통계량(함수) 안에 넣어 계산하여 구할 수 있다. 이 값이 중요한 이유는 이 값을 이용하여 귀무 가설을 기각할지 채택할지 결정하기 때문이다.

특별히 t 분포 상에서의 검정 통계량을 t-statistic(or t-value, t-통계량 혹은 t값)라고 한다.

즉, t-statistic은 t 분포를 따르며, t-Test에서 사용된다.

 

 

예시를 들어 검정 통계량의 개념을 이해해보자.

어떤 모집단이 있다. 모평균과 모표준편차를 알지 못하는 상태에서, 누군가가 이렇게 주장한다.

"모집단의 평균은 50이에요!"

 

가설을 미심쩍어하는 당신.

하지만 당신은 이 가설이 미심쩍다. 그래서 해당 가설을 검정하기 위해, 그 안에서 표본을 n개 추출해서 평균을 구해보았다. 그랬더니 $\bar{x}$가 나왔다. 과연 이 값은 가설을 기각시킬 수 있을까?

달리 말하면 저 $\bar{x}$가 아까 세운 가설을 기각 시킬 수 있을 정도로 유의미한 값일까?

 

위의 사례로 t-Test를 수행해보자.

귀무 가설($H_0$)과 대립 가설($H_1$)은 다음과 같이 놓을 수 있다.

$H_0$ : 모집단의 평균이 50 ($\mu=50$)

$H_1$ : 모집단의 평균이 50이 아님 ($\mu\ne50 $, 혹은 $\mu>50\ and\ \mu<50$ 이렇게도 표현 가능)

 

이 때 t-statistic는 어떻게 될까? t-statistic을 T라고 두자. 아까 전 검정 통계량의 정의에서 '귀무 가설이 참이라는 가정 하에' 얻은 통계량이라고 하였으므로, $\mu=50$이라는 것을 전제로 한다. 또한 t-statistic은 t분포를 따른다고 하였으므로 그에 따라 T를 구하면 다음과 같다.

$$  T = \frac{\bar{x} - 50} {\frac{s}{\sqrt{n}}}  $$

분자를 보면 알 수 있겠지만 $ \bar{x}$와 $\mu$가 많이 다를수록, 즉 차($\left| \bar{x} - \mu \right|$)가 클 수록 |T| 값은 커진다. 예를 들어 방금 전 구한 표본 평균 $\bar{x}$이 10이라면 |T|값은 $\bar{x}$가 30일 때보다 더 커질 것이다. 직관적으로 보면 10일 때가 30일 때보다 모평균이 50일 가능성은 더 희박해지는데, T값은 이와 상통한다.

반대로 차($\left| \bar{x} - \mu \right|$)가 작을수록 |T| 값은 작아진다. (혹은 표본 평균이 모평균과 동일하게 나왔다면 값은 0이 될 것이다.) 이는 직관적으로 보았을 때 모평균이 50일 가능성이 충분히 있다는 것을 보여준다.

 

t-statistic은 자유도가 n-1인 t분포 ($t_{n-1}$) 위에 있다. 이를 그림으로 나타내면 다음과 같다.

(T에 절댓값을 씌우는 걸 까먹었다. T=|T|라고 생각하고 보자.)

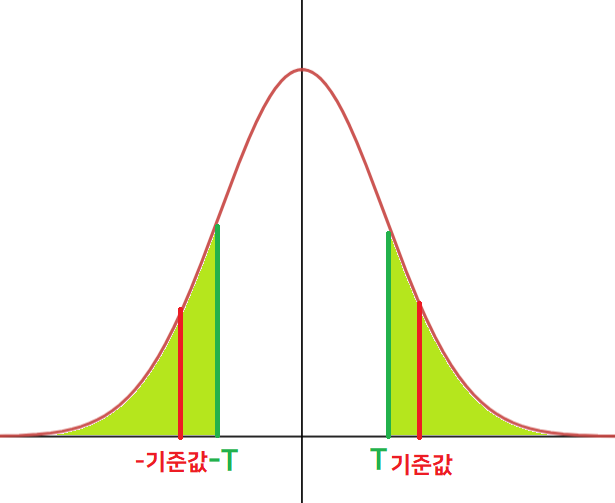
귀무 가설 채택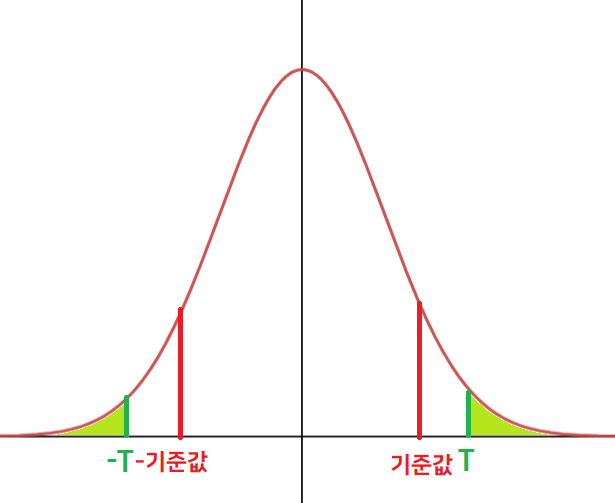

귀무 가설 기각

(참고로 위 그림에 나온건 정규분포지만 t분포 그래프는 너무 복잡해서 대충 비슷한 걸로 그렸으므로 그냥 넘어가자...)

 

$\bar{x}$이 $\mu$보다 크고 작은 건(=T의 부호가 양인지 음인지는) 별로 중요하지 않다. 우리가 알고 싶은 건 우리가 추출한 표본으로부터 구한 표본평균($\bar{x}$)이 모평균이 50이라는 가설을 부정시킬 수 있는가? 이고 그것을 구하기 위해서는 표본 평균과 모평균의 차이(절댓값)만 필요할 뿐이다.

그러므로 |T|와 -|T| 양 쪽에서 검정을 진행하는데, 이를 양측 검정(two-sided test)이라고 한다.

 

다르게도 생각할 수 있다, 아까 전 대립 가설이 $\mu \ne 50$ 이었고 이를  $\mu>50\ and\ \mu<50$라고도 쓸 수 있다고 하였다. 그렇기 때문에 검정통계량이 양 쪽으로(=양 쪽 중 하나로) 극단적인 값을 가지게 되면 직관적으로 귀무 가설보단 대립 가설에 가까워진다고 생각할 수 있고, 귀무 가설이 기각될 확률이 높아진다.

 

검정의 다른 종류로는 단측 검정(one-sided test)가 있는데 이는 추후에 설명하겠다.

 

 

귀무 가설을 기각할지 판단하기 위해서 어떤 '기준값'을 둬 보자.

우리가 구한 |T|값이 이 기준값보다 작으면, 표본 평균이 모평균에 근접했고 귀무 가설을 기각할 여지가 없다는 뜻으로 받아들이고 귀무 가설을 채택한다고 하자.

(|T| < 기준값   → 귀무 가설 채택)

반대로 |T|값이 기준값보다 크면 표본 평균과 모평균과는 꽤 차이가 있고, 귀무 가설을 기각할 여지가 충분히 있다는 뜻이므로 귀무 가설을 기각한다고 하자.

(|T| > 기준값   → 귀무 가설 기각)

 

'기준값'만 있으면 가설의 기각 여부를 판단할 수 있다. 기각 여부를 판단하기 위한 방법으로는 꽤 괜찮지 않은가?

실제로 가설 검정도 이와 동일한 (표현 방법은 다르지만) 방법을 사용한다. 그렇다면 저 '기준값'을 어떻게 선정하는지 알아보자.

 

 

2-3. 기각역(Rejection/Critical Region)과 p-value(유의 확률, significance probability)

기각역

앞서 언급한 '기준값'은 어떻게 선정하는가? 기준값을 선정한다는 것은, 기각역을 정하는 것과 동일하다.

기각역이란, 귀무 가설($H_0$)을 기각하는 영역을 말한다. 파트 2-2에서 |T|값이 기준값 바깥에 있을 경우 귀무 가설을 기각한다고 했었는데, 그렇기 때문에 기각역은 기준값 바깥의 영역이 된다.

그리고 여태까지 기준값이라고 불렀지만, 기각역과 보통 영역을 나누는 값을 임계값이라고 부른다.

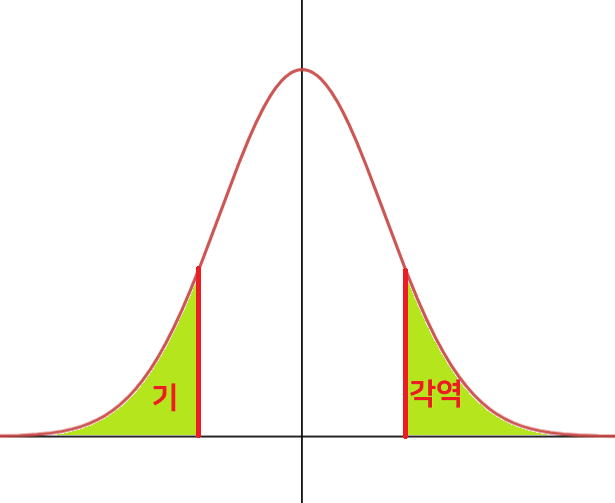
양측 검정의 경우. 단측 검정이면 기각역은 한 쪽으로 제한된다.

그리고 이 기각역은 유의 수준에 따라 결정된다. 즉 기각역의 확률값은 양 쪽 다 합쳐서 $\alpha$가 된다.

(단측 검정의 경우 한쪽의 면적만 $\alpha$가 된다.)

a = alpha이다. alpha 특수문자 쓰기가 귀찮았다....

이 기각역에 검정통계량이 들어올 경우, 귀무 가설은 기각된다.

여기까지 봤을 때, 당신은 이렇게 생각할지도 모르겠다.

 

'음. 그렇다면 2-2 파트에서 언급한 대로, 임계값과 검정통계량을 대소비교해서 기각 여부를 결정하면 될 것 같군.'

 

하지만 그것은 잘못된 생각이다. 그런 방법을 사용했다면, 굳이 복잡하게 기각역이라는 영역(region) 개념을 사용하지도 않았을 것이다. 통계에서는 검정 통계량을 기준으로 비교하지 않고, 이와 관련된 확률값을 기준으로 비교한다. 즉, T값 그 자체가 아닌 확률값 P(Y>|T|)로 비교를 하는 것이다! 기각역이라는 영역 개념을 사용하는 이유도, 바로 이 확률 비교를 위해서이다. 확률분포에서의 면적은 확률을 가리키기 때문에.

그리고 검정통계량(T)이 한번 더 가공된, 이 확률값 P(Y>|T|)을 p-value라고 부른다.

 

 

p-value란?

p-value는 귀무 가설이 맞다고 가정할 때, 얻은 결과(검정 통계량)보다 극단적인 결과가 실제로 관측될 확률이다. 간단하게 양측 검정일 경우 P ( Y > |T| ) 라고 이해하면 된다. 그림으로 나타내면 다음과 같다.

(사실 P (Y≥|T|)인지 Y>|T|인지 찾아보고 고민을 많이 했는데, 위에 내가 첨부한 영상은 Y>|T|라고 나와 있었고, 다른 곳에는 이에 대해 언급한 곳이 잘 없었다. 그리고 결국은 등호가 붙든 말든 값은 동일하니 별로 신경 쓸 필요가 없을 것 같다.)

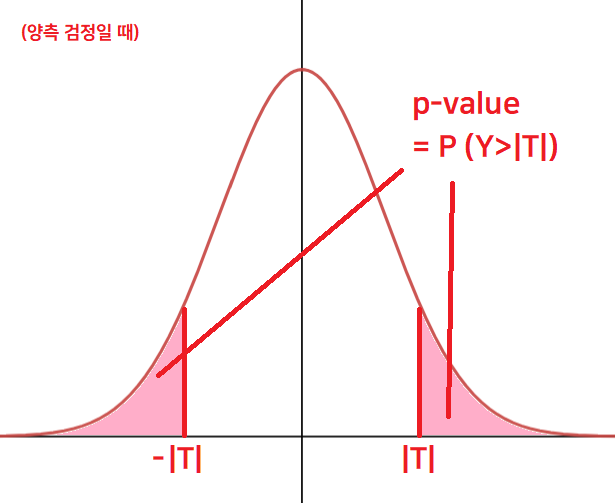
양측 검정의 경우

검정 통계량의 절댓값(|T|)이 커질수록 |T|는 양 끝으로 치우치게 되기 때문에 p-value는 작아진다. (|T| ↑ p-value↓)

 

 

이 p-value는 가설 검정에서 어떤 의미를 지닐까? 아까 전의 예시를 다시 가져와보자.

모집단이 있고, 귀무 가설은 $\mu = 50$이다. 당신은 이것이 미심쩍어서 모집단에서 표본 n개를 추출해서 표본 평균을 구했다. 그랬더니 45가 나왔다. 그러면 당신은 이런 생각을 할 수 있을 것이다.

"이것이 우연히 나올 수 있는 값인가? 아니면 우연이 아닌, 가설을 기각시킬 정도로 유의미한 값인가?"

 

당신은 이를 판단하기 위해서 가설 검정을 수행하기로 했다. 가설 검정의 절차에 따라 t-statistic을 구했고, $t_1$이라는 값을 얻었다고 하자. 이를 바탕으로 p-value(= P(Y > |$t_1$|))를 구했더니 0.15가 나왔다. p-value와 t-통계량의 정의에 따라 이 값의 의미를 최대한 간단하게 풀어 써보면 다음과 같다.

 

검정통계량의 절댓값이 |$t_1$|보다 클 확률이 0.15 =

"(s와 n이 고정되어 있다면) 모평균이 50이라는 것이 참일 때, 그 모집단에서 추출한 표본들의 평균이 45보다 작거나 55보다 클 확률이 0.15"

(혹은, 표본 평균이 45보다 작을 확률이 0.075라고 해도 된다.)

 

p-value에 대해 보편적으로 사용되는 해석에 따르면, p-value가 0.1을 넘으면 귀무 가설이 그럴듯하다고 한다.

(이 그림을 참조해보자. 근데 이 그림이 절대적인 기준인지는 잘 모르겠음)

그렇기 때문에 우리는 이렇게 생각할 수 있다.

"모평균이 50이라는 것이 참일 때, 표본 평균이 해당 값과 (같거나) 더 극단적인 값을 얻을 확률이 0.15(=15%)나 되는군. 그렇기 때문에 표본 평균이 45가 나오는 건 충분히 우연히 일어날 수 있는 일이야."

 

그러므로 모평균=50이라는 귀무 가설은 기각되지 않고 그래도 유지된다. (=귀무가설 채택)

 

 

하지만 위의 경우와는 달리, 똑같은 상황에서 표본 평균을 구했는데 그것이 45가 아니라 10이라고 하자. 그리고 t-statistic $t_2$를 구한 후 p-value를 구했더니 0.002가 나왔다고 하자. 이 의미를 간단하게 풀어 써 보면 다음과 같다.

 

검정통계량의 절댓값이 |$t_2$|보다 클 확률이 0.002 =

"(s와 n이 고정되어 있다면) 모평균이 50이라는 것이 참일 때, 그 모집단에서 추출한 표본들의 평균이 10보다 작거나 90보다 클 확률이 0.002"

(혹은, 표본 평균이 10보다 작을 확률이 0.001이라고 해도 된다.)

 

p-value에 대해 보편적으로 사용되는 해석에 따르면, p-value가 0.05보다 작으면 귀무 가설이 그럴듯하지 않다고 한다. 그렇기 때문에 우리는 이렇게 생각할 수 있다.

"모평균이 50이라는 것이 참일 때, 표본 평균이 해당 값과 (같거나) 더 극단적인 값을 얻을 확률이 0.002(=0.2%)밖에 안되는군. 이렇게 확률이 낮은 값이 실제로 나왔다는 건 우연이라고 보기는 힘들어."

 

"만약 우연이 아니라면, 답은 이거밖에 없네. 전제 자체가 잘못되었어. 즉, 모평균이 50이라는 전제(가설)이 애초에 잘못되었다는 거지. 그렇기 때문에 처음에 참이라고 가정했던 귀무 가설은 기각되어야 해."

 

그러므로 모평균=50이라는 귀무 가설은 기각된다.

 

 

즉 위의 예시를 다시 종합해보면 p-value가 낮다는 것은 해당 검정 통계량(+이보다 더 극단적인 값들)이 발생할 확률이 아주 낮은 값이라는 것이고, 더 들어가보면, 그럼에도 불구하고 이 값이 실제로 발생했기에 이 값은 가설 존립 여부를 결정하는 데 있어 무시할 수 없는 값(유의한 값)이 되는 것이다. 이름이 유의 확률(significance probability)인 이유가 있다.

 

물론 실제로 모평균은 50이 맞았고, 정말 운이 안좋게도 당신이 하필 골랐던 표본이 낮은 값들 뿐이라 표본 평균이 10이 나올 수도 있다. 즉, p-value는 확률일 뿐이지, "귀무 가설은 틀렸어!"를 절대적으로 말해주는 수치가 아니다. p-value가 낮아서 귀무 가설이 기각되어도, 귀무 가설이 참일 가능성은 존재한다.

 

또 p-value에 대한 흔한 오해가 하나 더 있는데, 'p-value는 귀무 가설이 참일 확률이다' 이다. 이런 식으로 생각하면 결과적으로는 맞겠으나, p-value에 대한 개념을 완전히 잘못 알고 있는 것이다. p-value는 귀무 가설이 참일 확률이 아니다!

(이 블로그에서 p-value의 개념과 흔한 오해들을 잘 설명해 두었다. 나도 참고를 많이 했다. 감사함니다..)

 

 

이제 p-value가 무엇을 말해주는지 감이 잡혔을 테니 다시 아까 전의 기각역 개념으로 돌아와보자. 아까 전 0.05, 0.1 등 p-value 값마다 보편적으로 통용되는 해석이 존재한다.

하지만 가설 기각 여부를 판단할 때는, 그냥 검정 통계량이 기각역에 위치하는지 (= p-value가 유의 수준보다 작은지) 만을 보고 기각을 하거나 채택을 한다. 즉 임계값(threshold)은 하나라는 것.

 

정리하면, 귀무 가설 채택 여부는 다음과 같이 판단한다.

$ p-value < \alpha $ ➔ 귀무 가설 기각 (검정 통계량이 기각역에 위치)

else ➔ 귀무 가설 채택

 

위에서 유의수준($\alpha$)은 일반적으로 0.05를 사용한다고 했다. 그렇기 때문에 보통 p-value가 0.05가 넘지 않을 경우 귀무 가설을 기각한다.

 

https://youtu.be/eyknGvncKLw

이 영상은 위와 같은 과정을 애니메이션으로 쉽게 풀어, p-value 개념을 보다 쉽게 설명했다. 영상 길이도 짧으니 한 번쯤 보는 것을 추천.

 

 

2-4. 가설 검정 과정 다시 정리

를 하기 전에,

t-통계량 식을 다시 보고 넘어가자.

$$  T = \frac{\bar{x} - \mu} {\frac{s}{\sqrt{n}}} = \frac {\left( \bar{x}-\mu \right) \sqrt{n}} {s} $$

식을 보면 t-통계량은 n에 비례하고, s에 반비례함을 알 수 있다.

즉 동일한 모집단에서 같은 표본 평균 값을 얻었어도 n이 클수록 |T|는 커져서 p-value가 작아지고,

s가 클수록 |T|는 작아져서 p-value는 커진다.

 

아까 전의 예시를 다시 가져와보자. 모집단에서 나는 표본을 10개 추출해서 40이라는 표본 평균을 얻었고, 당신은 표본을 1000개 추출해서 40이라는 표본 평균을 얻었다. 표본표준편차(s)가 동일할 때, p-value는 당신이 더 낮을 것이다. 만일 당신의 p-value가 유의 수준 0.05보다 작다면 모평균이 50이라는 가설은 기각될 것이다. (그리고 나의 경우 귀무 가설은 유지될 가능성이 높다.) 똑같은 표본 평균값을 얻었음에도 불구하고, 표본을 많이 추출해서 나온 당신의 값이 더 유의한 것이다.

 

이번에는, 모집단에서 나와 당신 모두 표본을 100개씩 추출했다. 그러나 나는 표본표준편차(s)가 1이고, 당신은 10이라고 하자. p-value는 이번에는 내가 더 낮을 것이다. 똑같은 표본 평균값을 얻어도, s가 작은(=표본 분산이 작은) 표본으로부터 나온 값이 더 유의할 가능성이 높다.

 

직관적으로 생각해보면 당연한 것이다. 표본의 개수를 최대한 많이, 또 수집한 표본들이 들쭉날쭉하지 않고 평균과 거의 비슷할 때, 거기서 나온 표본 평균이 더 신빙성 있는 값이라고 쉽게 짐작할 수 있지 않는가?

 

 

이제 진짜 가설 검정을 요약해보자.

1. 귀무 가설과 대립 가설을 수립한다. 보통 의심스러운 것을 귀무 가설로 두고, 자신이 증명하고자 하는 것을 대립 가설로 둔다. 그 후 유의 수준($\alpha$) 설정하는데 보통은 0.05로 둔다.

2. 모집단에서 표본을 추출한 후 가설 검정에 따라 어떤 검정 통계량을 설정할지 정한다. 여기에서 다룬 건 t-Test이기 때문에 검정 통계량으로 t-통계량을 사용한다.

3. 1에서 정한 유의 수준과 2에서 정한 검정 통계량의 종류(종류마다 따르는 분포가 달라짐)에 따라 기각역을 정한다. 여기서는 t-통계량이기 때문에 기각역이 t 분포상에서 정해진다. 양측 검정의 경우 양 쪽 면적을 합쳐서 $\alpha$가 되게 하기 때문에 한 쪽 면적은 $\alpha$/2가 된다.

4. 2에서 정한 통계량에 우리가 표본으로부터 구한 값을 넣어 검정 통계량을 구한다. 그리고 그에 따른 p-value를 구한다.

5. p-value가 유의수준보다 작으면 귀무 가설을 기각하고, 아닐 경우 귀무 가설을 채택한다.

 

 

2-5. 단측 검정

단측 검정은 양측 검정과 달리 기각역이 한 쪽에만 위치하는 검정을 말한다.

단측 검정과 양측 검정은 대립 가설의 모양에 따라 나뉘는데, 단측 검정의 가설 수립을 예시로 들면 다음과 같다.

$H_0 : \mu = 50 $

$H_1 : \mu < 50 $ (좌측 검정)

$H_1 : \mu > 50 $ (우측 검정)

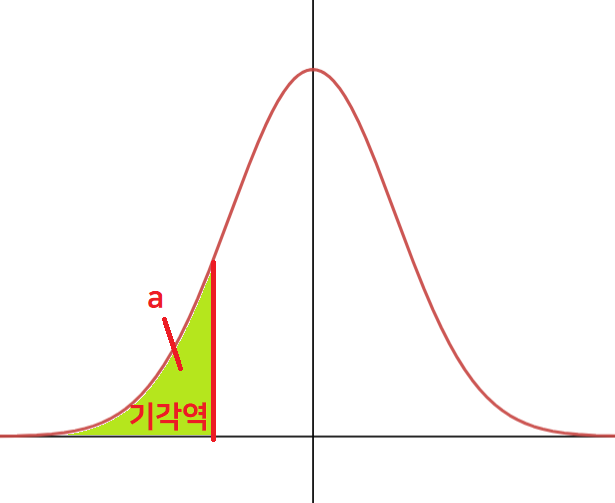
좌측 검정

우측 검정

좌측 검정의 대립 가설은 귀무 가설에서 주장한 값보다 더 작은 값을 주장하고,

우측 검정의 대립 가설은 귀무 가설에서 주장한 값보다 더 큰 값을 주장한다.

(양측 검정의 경우 둘 다 주장한다. 그렇기에 합해서 같지 않다($\ne$)를 주장하는 것이 된다.)

 

왜 이렇게 되는지는 다음과 같이 생각하면 직관적으로 이해할 수 있다.

아까 전 p-value에 대해 설명할 때, 값이 충분히 작으면 그 값은 유의하다고 했었다.

예를 들어 좌측 검정에서 귀무 가설이 모평균=50이라면, 대립 가설은 모평균 < 50이 될 것이다.

이 경우 표본 평균이 모평균보다 작을수록 검정 통계량이 의미있는 값을 지닐 가능성이 커진다. 그러나 일단 표본 평균이 모평균보다 크면(검정 통계량이 양수가 되어 오른쪽에 있게 됨), 검정 통계량은 그것이 얼마나 크든 양측 검정과는 달리 의미를 가지지 않는다. 왜냐하면 그 값은 대립 가설을 지지하는 증거가 되지 못하기 때문이다.

 

단측 검정의 경우 양측 검정과 달리, 기각역이 한 쪽 뿐이므로 기각역 한 쪽의 면적이 $\alpha$이다.

 

 

3. t-test for slope (기울기에 대한 가설 검정)

이제 이 t-test를 선형 회귀의 기울기에 적용시켜 볼까. (쉬운 이해를 위해 단순선형회귀라고 가정하겠다.)

 

우리가 구한 선형 회귀 coefficient값에는 한계가 있다. 

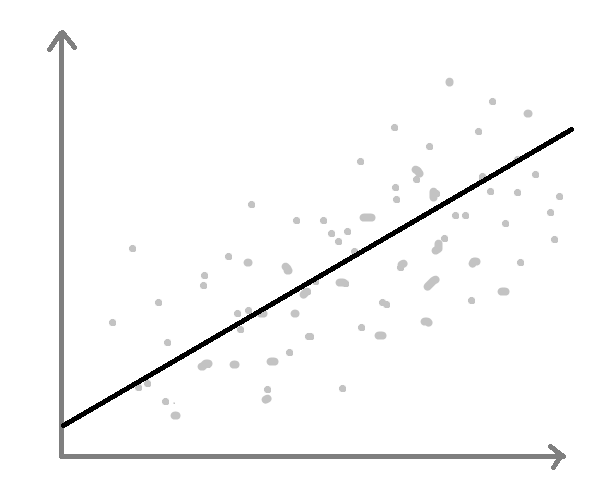
$ \widehat{Y} = \beta_0 + \beta_1 X $ <모집단에서 회귀식을 구함>

$ \widehat{Y} = \widehat{\beta}_0 + \widehat{\beta}_1 X $ <표본 n개를 추출해서 회귀식을 구함>

보다 정확한 회귀식을 구하려면 모집단 전체를 대상으로 모델링을 해야 하는데, 그러기는 현실적으로 불가능하기 때문. 그 대신 우리는 모집단 중 일부를 추출해서(표본) 회귀식을 만든다.

그렇다면 여기서 의문이 하나 생긴다.

"우리가 구한 기울기($\widehat{\beta}_1$)가

모집단에서도 X와 Y의 연관 관계를 설명할까?"

 

극단적이지만 이런 경우가 생길 수도 있을 것이다.

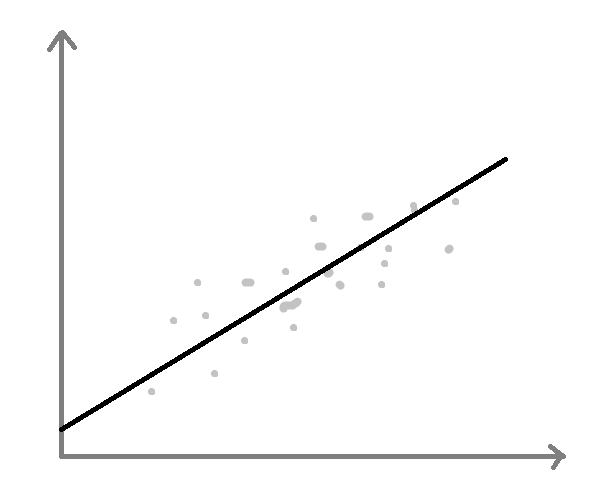
표본

실제 모집단

이렇게 되면 우리가 구한 회귀식은 모집단의 독립 변수(X)와 종속 변수(Y)의 관계에 대해 완전 잘못 설명한 것이 된다. 물론 이런 일이 일어날 가능성은 매우 낮을 것이다. 그렇지만 단순히 "이런 일이 일어날 확률은 낮으니까 이 회귀식은 그럴듯해~"라고 하는 것보다는 정확한 통계적 근거를 들어 "이 회귀식은 그럴듯해~"라고 하는 것이 더 엄밀하고 논리적이지 않을까?

 

 

이런 이유로 우리는 선형 회귀의 기울기(slope)에 대해 t-test를 수행한다.

 

0. 선형 회귀의 전제 조건 (참조1 참조2)

• X와 Y는 선형 관계이다.
• 어떤 X 값 하나가 주어졌을 때,
  • Y 값들은 독립적이다. ($ Cov \left( y_i, y_j \right) = 0 $)
  • Y 값들은 대략적인 정규 분포를 따른다. (단, 표본의 크기가 클 경우 약간의 비대칭은 허용)

• 각 X에 대해, Y의 확률 분포는 동일한 표준 편차 $\sigma$를 가진다.
  • 잔차의 분산 또한 동일하다. ($ \epsilon \sim N \left( 0, \sigma^2 \right) $ )
• 즉, y는 다음과 같은 분포를 따른다.

$$ y_i \sim \left( \beta_0 + \beta_1x_i,\ \sigma^2 \right) $$

증명 (다만 여기선 조건부 분포(?) Y|X를 구했다. 근데 의미상 한 X에 대한 y의 분포이니... 의미상으론 우리가 구하고자 하는 것과 똑같은 것 같음.... 으으 통계는 어려워)

 

여기서 유심히 봐야할 부분은

y의 평균이, 모집단 전체를 대상으로 구한 (불가능하겠지만) 회귀식으로 예측한 값과 동일하다는 것과

y의 표준편차가 에러($epsilon$)의 표준편차와 동일하다는 것.

 

 

1. 가설 수립과 유의 수준 설정

먼저 가설을 수립해야 할 것이다. 주로 주장하는 내용을 대립 가설에 넣으므로, 대립 가설에 '(모집단에서도) X와 Y는 연관이 있다.' 즉 (최소제곱법에 의해 선형회귀식이 알맞게 구해졌을 경우) 'X와 $\widehat{Y}$는 선형 관계이다.'가 들어갈 수 있을 것이고, 반대로 귀무 가설에 'X와 $\widehat{Y}$는 연관이 없다.'가 들어갈 것이다.

 

• 귀무 가설($H_0$) : X와 $\widehat{Y}$는 선형적인 연관이 없다.
• 대립 가설($H_1$) : X와 $\widehat{Y}$는 선형 관계이다.

 

X와 $\widehat{Y}$가 선형적인 연관이 없는 경우

X와 $\widehat{Y}$가 연관이 없다는 뜻은, 위 그림처럼 X와 Y가 연관성이 존재하지 않아 X와 $\widehat{Y}$ 사이에 선형적인 관계가 성립하지 않는다는 뜻이다. 즉, slope=0이 된다는 뜻이다.

그렇기 때문에 가설을 다음과 같이 고쳐쓸 수 있다.

 

• 귀무 가설($H_0$) :  $ \beta_1 = 0 $
• 대립 가설($H_1$) :  $ \beta_1 \ne 0 $

 

수립된 가설에 의거하여 t-test의 목적을 서술하면 다음과 같다.

 

"우리가 구한 기울기($\widehat{\beta}_1$)가 $ \beta_1 = 0 $ 이라는 귀무 가설을 기각시킬 정도로 유의미한 값일까?"

 

아까 전 모평균을 구한 것과 되게 비슷한 레파토리이지 않은가? '모평균=50'대신 '$\beta_1 = 0$'이 들어갔을 뿐이다.

 

보통 유의 수준은 0.05로 설정한다. 우리도 $\alpha = 0.05$라 두자.

 

2. 표본 추출과 검정 통계량 설정

모집단 속에서 n개의 표본을 추출한다. n개의 (X, Y)를 가진 집합이 될 것이다. 이 데이터를 바탕으로 글 선형 회귀(1)에 나온 방법으로 slope를 구한다.

 

검정 통계량은, 아까 언급했듯 t-test이므로 t-통계량을 사용한다.

$$  T = \frac{\bar{x} - \mu} {\frac{s}{\sqrt{n}}} = \frac {\left( \bar{x}-\mu \right) \sqrt{n}} {s} $$

그런데 여기서 또 의문이 생긴다.

"$\mu$와 s에는 무엇이 들어가야 하지? 대체 $\widehat{\beta}_1$의 모평균과 표준편차가 뭔데?"

 

$\mu$와 s, 여기에 무엇이 들어가야 하는지 설명하기 위해 slope만의 t-statistic 식을 유도해보자.

 

아까 0. 선형 회귀의 전제 조건에서 Y는 정규 분포를 따른다고 했었다,

$$ y_i \sim \left( \beta_0 + \beta_1x_i,\ \sigma^2 \right) $$

그리고 $\widehat{\beta}_1$는 y에 대한 선형 결합으로 표현되므로, $\widehat{\beta}_1$도 정규 분포를 따르리라 짐작할 수 있다. 실제로 $\widehat{\beta}_1$는 다음과 같은 분포를 따른다.

$$ \widehat{\beta}_1 \sim N \left( \beta_1, \frac{\sigma^2}{S_{XX}} \right)  $$

증명은 이 블로그에 잘 나와있다. 참고하자.

 

이제 감이 잡힐 것이다. 만약 검정 통계량을 t 분포 상에서가 아닌 정규분포 상에서 구한다면, 검정 통계량이 다음과 같을 것이다.

$$ Z = \frac {\widehat{\beta}_1 - \beta_1} {\sqrt{\frac {\sigma^2}{SS_{XX}} } } $$

 

$\beta_1$은 모평균의 추정과 동일하게, 우리가 구해야 하는 값이니 그렇다치고... 문제는 우리는 모집단을 모르기 때문에 모표준편차($\sigma$)도 모른다는 것이다. 하지만 이제 당신은 이 문제를 어떻게 해결해야 할지 짐작이 갈 것이다.

 

"오호라, 그렇다면 $\widehat{\beta}_1$이 정규 분포를 따른다는 것을 알았으니, 이를 지지고 볶으면 t-통계량도 구할 수 있겠군. 아까처럼 t-통계량에서는 모표준편차 대신 표본표준편차를 쓸 거니까, 모표준편차 문제를 해결할 수 있겠어."

 

그렇다. 실제로 slope의 t-statistic 식은 아래와 같다.

$$  T = \frac {\widehat{\beta}_1 - \beta_1} {\sqrt{\frac {\widehat{\sigma}^2}{SS_{XX}} } }  \sim t_{n-2}$$

$$ = \frac {\widehat{\beta}_1 - \beta_1} {\sqrt{\frac {SE}{SS_{XX}} } }  $$

$$ = \frac {\widehat{\beta}_1 - \beta_1} {SE \left( \widehat{\beta}_1 \right) }  $$

 

증명은 모분산과 표본분산의 비율이 카이제곱분포를 따른다는 것을 이용하면 된다. ($\frac {\widehat{\sigma}} {\sigma} \sim \frac {\chi^2_{n-2}} {n-2} $ ) 자세한 사항은 아까 첨부했던 곳을 또 참조하길 바람.

 

저 식을 보면 우리가 왜 글 (2)에서 Standard Error of Estimate를 구하려 했는지, SE of Slope를 구했는지 알 수 있다. 여기에 사용되기 때문이다. 우리가 추출한 표본을 이용하면 SE of Slope를 손쉽게 구할 수 있다.

그리고 아까 우리는 $\beta_1 = 0$ 인지 아닌지를 기준으로 가설을 세웠으므로, $\beta_1 = 0$라는 귀무 가설을 바탕으로 검정 통계량을 설정해야 한다. 그렇기 때문에 최종적으로 검정 통계량의 식은 다음과 같이 된다.

$$ T = \frac {\widehat{\beta}_1 - 0} {SE \left( \widehat{\beta_1} \right) }  $$

 

이 식의 $\widehat{\beta}_1$에 내가 구한 slope값을 넣어 주면 된다.

 

 

3. 기각역 설정

대립 가설이 $\ne$ 꼴이므로 양측 검정을 사용한다. 그러므로 기각역은 아래와 같이 t 분포의 양쪽 면적이다.

유의 수준을 0.05로 설정했으므로 한쪽 면적은 0.05 / 2 = 0.025가 된다.

p-value가 유의 수준보다 작으면, 즉 검정 통계량이 기각역 안에 들어왔을 때, 귀무 가설을 기각한다.

 

 

4. 통계량 계산

검정 통계량을 계산하고, 이를 이용해 p-value를 계산한다.

예를 들어 내가 추출한 표본에서 구한 선형 회귀식의 기울기가 a이고, SE of slope가 b라고 하자. 그럼 검정 통계량이 다음과 같이 된다.

$$ T = \frac {a - 0} {b}  $$

이 때 p-value는 다음과 같다.

$$ p\text{-}value = P\left(Y > \left|T\right| \right) $$

정규 분포의 면적을 직접 적분하기 어려웠던 것처럼, p-value값을 직접 구하기는 어렵다. 대신 t-table을 사용한다.

 이미지 출처

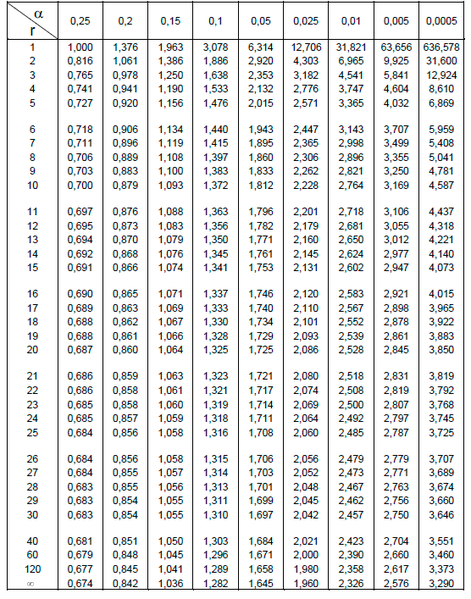
열($\alpha$)은 유의 수준, 행(r)은 자유도이다. 만일 내가 20개의 표본을 추출했을 경우 단순 선형회귀이므로 자유도는 20-2 = 18이 된다. 행에서 18을 찾고 유의 수준이 0.05이므로 열에서 0.05를 찾은 후, 둘이 만나는 지점의 값이 바로 기준값의 t-statistic이 된다.

예시의 경우에는 1.734가 나오는데 내가 구한 검정 통계량이 이보다 크면 귀무 가설을 기각한다.

즉, 검정 통계량이 이 값보다 클 경우 내가 구한 선형회귀식의 기울기는 유의미하다는 것이 된다. (=X와 Y가 연관이 있을 가능성이 높다.)

 

 

4. 신뢰 구간 (Confidence interval)

글의 첫 부분(1-1)에서 '모평균 추정'을 다룬 적이 있었다. 기울기(slope)의 신뢰 구간도 이와 동일하게 구할 수 있다. 한 가지, 정규 분포가 아닌 t 분포 상에서 구해야 한다는 점만 빼고.

 

각 기호가 가지는 의미가 무엇인지는 이제는 잘 알고 있을 것이라 본다. 그리고 모평균 추정에서 이미 충분한 설명을 했기 때문에 자세한 설명은 생략하겠다.

 

신뢰 수준이 $100 \left( 1 - \alpha \right)$일 때, 기울기의 신뢰 구간은 다음과 같다.

$$ \widehat{\beta}_1 - t_{\alpha/2, n-2} \sqrt{\frac{\widehat{\sigma}^2}{SS_{xx}}}\ \le\ \beta_1\ \le\ \widehat{\beta}_1 + t_{\alpha/2, n-2} \sqrt{\frac{\widehat{\sigma}^2}{SS_{xx}}}  $$

 

위의 식은 t-statistic을 신뢰 수준 영역의 경계에 있는 t값과 비교한 식에서 도출할 수 있다.

$$ \left| T \right|\ \le\ t_{\alpha/2, n-2}  $$

 

 

5. 실제로 통계 수치를 분석해보자!

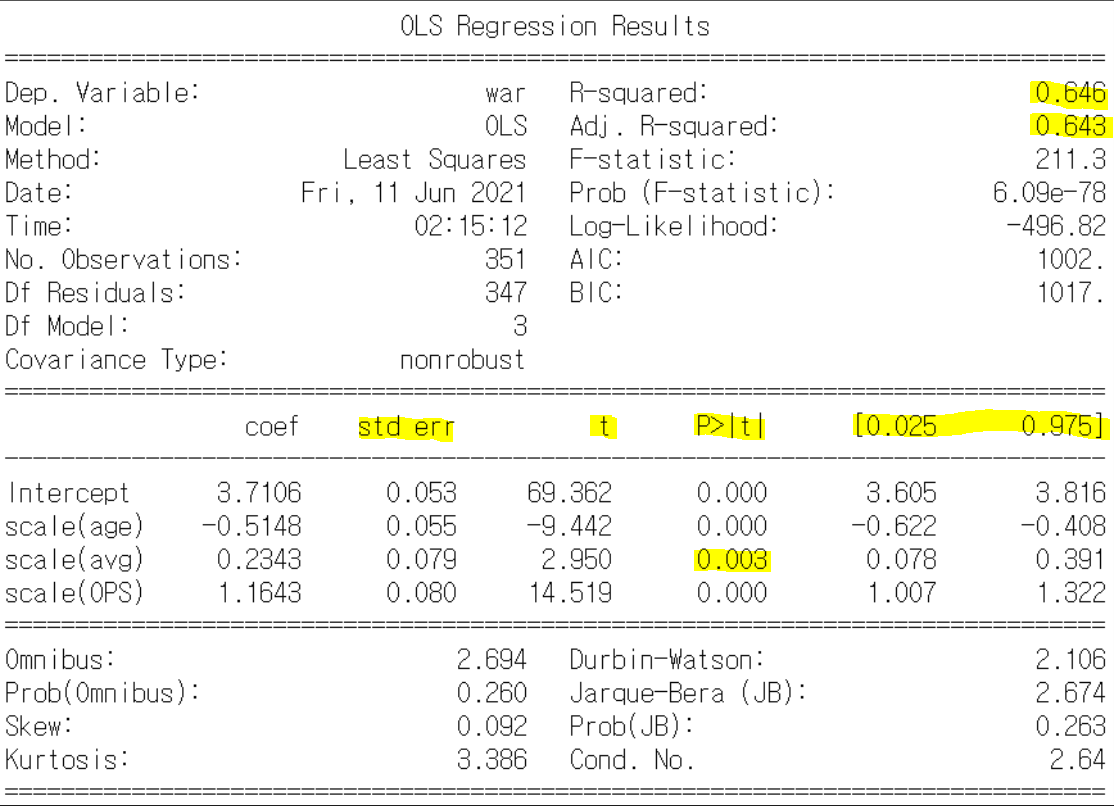
kbo 선수들 중 규정타석을 채운 선수들의 나이, 타율, OPS와 war간의 상관 관계를 분석

(분석을 위해 사용한 데이터 출처는 여기.)

0. 에서 언급했던 분석 결과를 다시 가져왔다. 형광펜 친 부분은 지금까지 공부했던 부분이다. 어떤 의미를 가지는지 살펴볼까. 이를 볼 수 있으면 선형 회귀가 잘 되었는지 제대로 되지 않았는지 알 수 있다. (근데 나도 사실 잘 모른다는 건 함정.....ㅎ)

• R^2(결정계수) = 0.646. 결정 계수가 어느 정도 되어야 유의하다고 볼 수 있는가?에 대해 찾아봤는데, 분야마다 기준이 다 다르고, 사람마다 말이 달랐다. 그래도 반올림해서 0.65정도면 설명력이 나쁘진 않은 것 같다. 실제로도 각 x와 real y 사이에 scatter plot을 그려 보았는데 age의 경우를 제외하고는 꽤나 강하게 선형적인 관계를 보이긴 했다.
• std err : 이건 수치 보다는 이런 식으로 coeffieicnt마다 SE 값을 구해준다~를 보여주고 싶어서 형광펜을 그었다.
• t : 검정통계량. (더 좁게는 t-통계량.) t 테이블과 비교해보니 average 제외하고는 다들 임계값과 한참 멀리 떨어져 있어서 유의하지 않은 걱정은 하지 않아도 되겠구나. 싶다.
• P > |t| : p-value. 역시 예상했던 대로 다른 coefficient들은 zero에 가까운 값이 나왔는데, avg만 0.003이 나왔다. 꽤나 낮은 값이라 다행히 귀무 가설은 기각되었지만, 여전히 의구심이 남는다. 나이와 타율 중, war(대체 선수 대비 승리 기여도)와 더 연관이 있는 건 직관적으로 보면 당연히 후자일 텐데 왜 p-value는 전자가 더 낮게 나왔는지... 물론 p-value가 각 coefficient의 설명력을 말해주는 수치가 아님은 아주 잘 알고 있다. 다만 선형 회귀를 많이 다뤄보지 않아서 조금 알쏭달쏭하다. 이것도 공부를 더 하면 자연스레 받아들일 수 있을까.
• [0.025 0.975] : 신뢰수준 95%에서의 신뢰 구간. 저 구간안에 모집단의 coefficient 값이 있을 수도 있고, 없을 수도 있고? 하지만 데이터 특성 상 전수조사가 가능하기도 하고, 이미 이 분석은 모집단 중 80% 이상을 표본으로 뽑아 분석한 것이기 때문에 저 구간 안에 있을 확률이 굉장히 높지 않을까....... 싶다.

 

 

읽어 주셔서 감사합니다.

오탈자, 틀린 부분은 댓글로 언제든지 지적해주세요.

 

 

 

 

참고한 자료

학교 <데이터사이언스개론> 수업 강의 자료

[핵심 머신러닝] 선형회귀모델 3 (파라미터 구간추정, 가설검정)

bskyvision - 모평균의 신뢰구간 추정하기

공돌이의 수학정리노트 - 신뢰 구간의 의미

공돌이의 수학정리노트 - t-value의 의미와 스튜던트의 T 테스트

2-07 Chapter 02 모집단과 표본추출(모집단과 표본추출방법) : 제대로 시작하는 기초통계학

행복한엄쌤의 블로그 - [통계교육] 풀어쓰는 통계 - t 검정(t-test)이란?

통계의 본질 - [통계 기초] 24. 통계적 가설 검정 감잡기 4 (양측검정 vs 단측검정)

P-value in statistics: Understanding the p-value and what it tells us - Statistics Help

블로그 진화하자 - 어디에도 소속되지 않기 - p-value란 무엇인가

Hypothesis Test for Regression Slope

data science, statistics - [회귀] 단순회귀분석에서의 구간추정과 가설검정

jangpiano님 블로그 - [회귀] Method of least squares - 최소제곱법 / 단순 선형 회귀모형/ 특성 / 가우스 마코브 정리

jangpiano님 블로그 - [회귀] 단순회귀분석에서의 구간추정과 가설검정

Simple Linear Regression

stack exchange - How is Y Normally Distributed in Linear Regression [duplicate]

EG공간 - 기울기값과 회귀선에 대한 추론