Back-Propagation (오차 역전파법) : 논문을 바탕으로 개념 정리

딥러닝을 배운다면 필수로 알고 있어야 하는 백-프로파게이션-! 그러나 학교 강의마다, 관련 도서들마다 내용은 비슷비슷한데 수식, 기호 표기가 달라서 지식들을 하나로 취합하기가 여간 쉬운 게 아니더라.. (+내가 도형, 기호 등에 약함)

그래서 그냥 원래 논문을 보고 정리하기로 했다. 우리 학교 딥러닝 분야 강의 교수님들도 이 논문은 꼭 읽어보라고 추천해주시기도 했고 해서, 이번 기회에 정말 오랜만에 (이젠 꾸준히 읽어야지...^^ㅠ) 논문이란 걸 읽어보았다.

 

참고 논문 :

David E. Rumelhart, Geoffrey E. Hinton & Ronald J. Williams

    - Learning representations by back-propagating errors (1986)

 

서론

우리 학교 교수님 피셜 정말 유명한 논문이라고 한다. (당연함. 피인용수가 27000건이 넘음.) 이 논문이 나오기 전까지만 해도 '딥 러닝'이라는 개념만 있었고, 상용화된 건 hidden layer 없이 단순히 퍼셉트론을 학습시켜 값을 나타내는 정도에 불과했다고 한다. 왜냐하면 output layer에서는 MSE나 cross-entropy등을 쓰면 loss를 수식적으로 표기할 수 있지만, hidden layer의 경우에는 그 층의 unit의 actual result를 알지 못하기 때문에 loss를 구할 수 없었기 때문이다.

그러나 이 논문이 발표되고 난 후로 back-propagation이라는 개념이 생겼고, hidden layer가 존재해도 가중치를 갱신할 수 있게 되었다. 기존 퍼셉트론은 선형 경계밖에 표현하지 못하였는데, hidden layer가 추가되면서 두 직선, 더 나아가 모든 형태의 결정 경계를 표현할 수 있게 되었다.

(저는 학교 수업에서 이렇게 배웠었는데, 혹시 틀린 내용이 있을 경우 댓글로 지적 바랍니다.)

 

 

들어가기 전에 : chain rule과 tree diagram 짚고 넘어가기

시험 준비를 하면서, 처음으로 미적분학을 끝까지(그러니까 다변수 파트까지) 공부하게 되었고, 이것을 배우기 전과 후로 머신러닝 분야에서 보는 시각이 많이 달라졌다. 밑빠진 독이었던 내가, 그 구멍이 채워진 느낌이 들었다고 해야 하나. (더불어 인공지능 분야를 희망한다면 무조건 기초 수학(미적분, 선대, 통계)이 뒷받침되어야 한다는 것을 깨달았다.)

이번 논문을 읽을 때도 공부했던 미적분학 지식에서 많은 도움을 받았는데, 그 중 chain rule에 한번 더 짚고 넘어가고자 한다. 우선 대충이나마 back-propagation을 접해본 사람은 알겠지만 처음부터 끝까지 chain rule만 쓰다 끝난다. 퍼셉트론의 특성상 변수가 많아질 수밖에 없기에, 여기다가 chain rule을 적용하면 필연적으로 헷갈릴 수밖에 없다. (물론 선천적으로 이런 기호 등을 다루는 데 타고난 사람이라면 해당되지 않을 수도..? 일단 난 아니다.)

다행히도 이런 사람들이 꽤 많았는지 수학자들이 tree diagram이라는 걸 고안해두었다.

tree diagram이란?

함수와 변수들간의 관계를 간단하게 tree형태로 표현한 그림이다. 예시를 보면 이해가 쉬울 것이다.

ex1. $y=f(x),\ x=g(u)$

y는 x에 대한 함수이며, x는 u에 대한 함수이다. 이를 tree로 나타내면 다음과 같다.

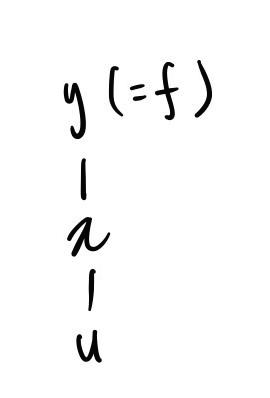
그다음으로는 다변수 함수를 보자.

ex2. $z=f(x,y),\ x=g(u,v),\ y=h(u,v)$

z는 x,y에 대한 함수이며 x,y는 u,v에 대한 함수이다. 여기에서, x와 y, u와 v는 독립변수임을 알 수 있다. (즉, x를 y에 대해 미분하면 0) 이럴 경우 tree의 가지를 나눠 두 독립변수를 각각 따로 적어준다.

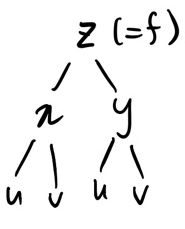
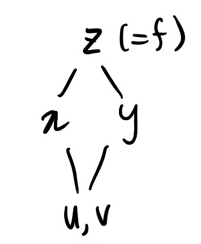
(좌 : 정석, 우 : u,v를 중복 되게 두 번 적기 귀찮을 때 편법(이 글에서는 이 표기를 더 많이 사용함))

 

이렇게 복잡한 함수를 tree로 나타내면, 변수들 간의 관계를 좀 더 쉽게 파악할 수 있고, chain rule 적용도 간단해진다.

예를 들어, ex1의 함수에서 $\frac{\partial{f}}{\partial{u}}$를 계산해보자.

u에 대해 편미분 했으므로 u가 도착 위치이고, f를 편미분했으므로 f(=y)에서부터 시작한다. 시작점부터 tree를 따라 u까지 쭉 내려가며 거치는 변수들을 식에 곱셈 형태로 추가해주면, chain rule에 의거하여 미분식을 변형한 것이 된다.

ex2의 함수에서도 $\frac{\partial{f}}{\partial{u}}$을 계산해보자. 여기서 한 가지 tree의 성질이 적용되는데,

tree를 거치다 자식 node가 두 개 이상 (즉, 가지가 갈라지는 경우)를 만나면 :

1. 한 가지 아래에만 목표 변수(도착 지점)가 있는 경우

ex1. 과 동일하게 진행해주면 된다.

2. 두 개 이상의 가지 아래에 목표 변수가 있는 경우

우선 한 갈래를 선택해 전진하며 도착 지점까지 곱셈을 진행하고, 똑같이 다른 한 갈래를 선택해 도착 지점까지 곱셈을 진행한다. 이렇게 모든 갈래를 거친 곱셈 식들을 모조리 더해주면 된다.

 

정리하면 부모-자식 노드는 곱셈, 형제 노드는 덧셈의 관계를 가진다고 보면 된다.

내가 말주변이 없어 조리 있게 설명하지 못한 것 같아 이해가 어려울 수도 있다... 예제를 보며 다시 이해해보자.

 

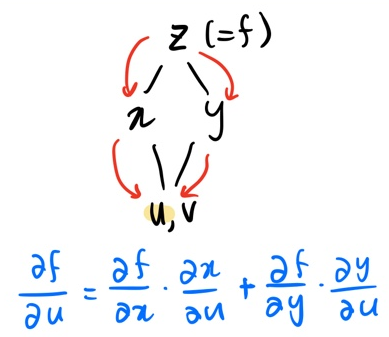
한 방에 이해되지 않는가? 역시 백문이 불여일견!!

여기서 u, v도 가지로 갈라지는데 왜 더하지 않느냐고 할 수 있는데, 애초에 u와 v는 독립 변수이기 때문에, u로 편미분 할 때는 v는 그냥 없는 변수 취급해도 된다. 

tree를 사용하면 합성함수 여부와 변수 간의 관계를 머리 아프게 일일이 생각하지 않아도 손쉽게 편미분을 할 수 있다.

 

 

Forward Pass : 신경망이 가지는 수식의 형태

feed-forward network(순방향 신경망)을 기준으로 설명을 진행하고자 한다.

(사실 RNN 등은 아직 자세히 안 배워서 모름..^^ 논문에서도 FFN을 예시로 들었기에 그대로 간다..!!!)

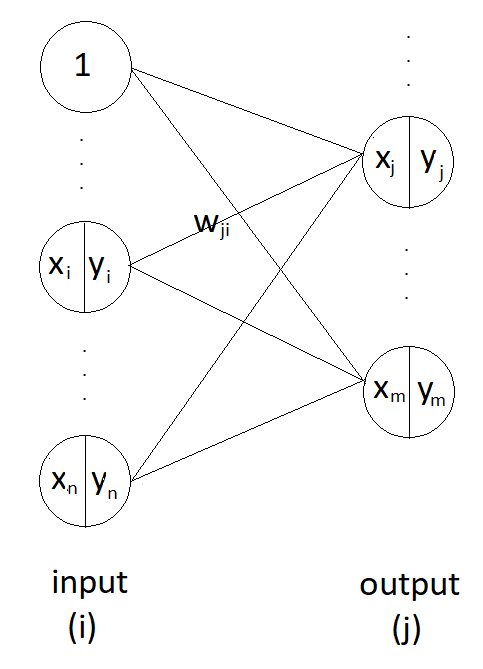
이런 구조의 신경망이 있다고 하자. hidden layer는 없고, input, output 두 개의 층으로 구성되어 있다. 그림에서 표시된 unit은 일부이므로 connection(실선) 또한 일부분만 표시되었다.

input layer의 임의의 unit의 인덱스를 i, output layer의 임의의 unit의 인덱스를 j라 하자. 그리고 input layer의 i번째 unit과 output layer의 j번째 unit를 잇는 가중치 값을 $w_{ji}$라 하자.

input layer의 unit 수를 n개, output layer의 node 수를 m 개라고 하자.

input layer와 output layer의 activation function은 sigmoid 함수이다.

 

위와 같은 조건에서 output layer의 unit $x_j$ 값을 수식으로 나타내면 다음과 같다.

$$ x_j = \sum_{i} y_iw_{ji} $$

activation function이 sigmoid라고 하였으므로 $y_j$의 값은 다음과 같다.

$$ y_j = \frac{1}{1+e^{-x_j}} $$

 

loss function으로 MSE를 사용한다고 하자. 그러면 total error $E$는 다음과 같다.

$$ E = \frac{1}{2} \sum_{c} \sum_{j} \left( y_{j,c} - d_{j,c} \right)^2 $$

여기서 y는 신경망을 통해 도출된 값, d는 실제 결괏값이다.

c는 case 개수=sample 수 인데, 쉽게 말해서 학습시키고 있는 데이터의 수라고 보면 된다.

 

물론 실제 연산에서는 빠른 속도를 위해 GPU를 이용, 병렬적으로 수행되기 때문에 (전문적인 용어로 GPGPU라고 한다... 라고 아는 척을 해보았다.) 행렬이 사용된다. 그러나 논문에서는 행렬 개념이 사용되지 않았고, (왜일까?) 이 글도 역전파에 중점을 두고 있기 때문에 행렬 없이 수식을 전개시켜 보았다.

 

 

Back-Propagation : (1) hidden layer가 없을 때

이 논문에서는 optimizer로 BGD(Batch Gradient Descent), 그중 momentum 기법을 사용한다. (자세한 식은 후술)

그러므로 E를 minimize 하게끔 가중치를 갱신하기 위해서는 위해서는 각 weight에 대한 E의 편미분 값($\frac{\partial{E}}{\partial{w}}$)을 찾아야 한다. 그리고 이를 찾는 데에 chain rule이 적용된다.

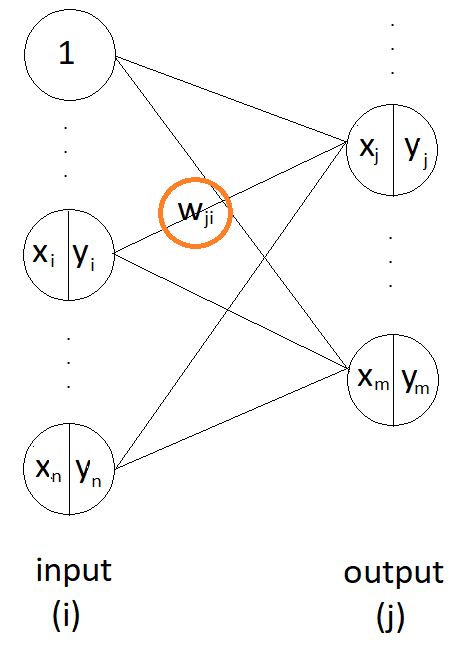
동그라미 친 가중치에 대한 E의 편미분 값을 찾아야 한다.

 

E에 대한 tree diagram 그리기

우선, 위의 그림처럼 hidden layer 없이, input layer와 output layer로만 구성된 신경망에서 가중치를 갱신해보자.

E는 여러 변수들로 구성되어 있으므로, 하나의 함수로 볼 수 있다. 이때 E를 하나의 case에 대한 loss로 가정해도 (즉, $ E = \frac{1}{2} \sum_{j} \left( y_{j,c} - d_{j,c} \right)^2 $ 로 봐도) 무방하다. 왜냐하면 $\left( \sum f(x) \right)' = \sum f'(x) $ 이 성립하므로, 하나의 case에 대해 미분한 결과식에 값만 다르게 넣어 $\frac{\partial{E}}{\partial{w}}$를 계산한 후 더해주면 되기 때문이다.

$$ \frac{\partial{E}}{\partial{w}}_{total} = \sum_{c} \frac{\partial{E}}{\partial{w}} $$

 

chain rule을 쓰기 위해 E에 대한 tree를 그려보자.

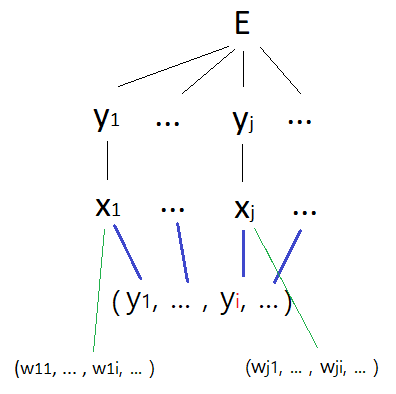
갑작스럽게 이 그림을 보면 이해가 안 될 수도 있으므로 직접 tree를 그려보는 것을 권장한다.

d는 상수 취급한다. 그러면 E는 $y_j$들로 구성된 함수이므로, m개의 가지를 가진다. 각 $y_j$들은 $x_j$에 대한 sigmoid 함수이므로 자식 노드로 $x_j$를 가지며, 이는 일변수 함수이므로 가지가 갈라지는 것 없이 오직 하나의 x를 갖는다.

그다음부터가 중요한데, 우선 초록 가지부터 보자.

$ x_j = \sum_{i} y_iw_{ji} $ 이므로 $x_j$는 해당 unit으로 모이는 weight ($w_{j1}$ , ... , $w_{ji}$ , ...) 에 대한 함수이다. (원래 각 w값마다 가지를 달아주어야 하나 생략했다.)

이 $w_{ji}$는 index에서부터 알 수 있듯이 각 $x_j$마다 별개의 $w_{ji}$를 변수로 가진다.. tree를 보면 이를 쉽게 파악할 수 있을 것이다.

그다음으로 파란 가지를 보자.

index에서 짐작할 수 있듯이 w와는 다르게, $y_i$는 $x_j$가 달라도 동일한 $y_i$를 변수로 가진다.

(이 부분이 이해가 가지 않으면 $ x_j = \sum_{i} y_i w_{ji} $ 식을 다시 한번 살펴보도록 하자.)

 

tree를 바탕으로 $\frac{\partial{E}}{\partial{w}}$ 구하기

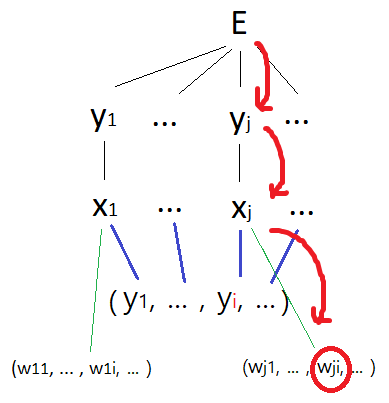
E를 편미분 했으므로 E에서부터 시작한다. $w_{ji}$에 대해 편미분했으므로 도착 지점은 빨간 동그라미 친 부분이 된다. tree 모양이 복잡한 만큼 도중에 많은 변수들을 거쳐야 할 것 같지만, 수많은 $y_j$ 가지들 중 한 가지에만 목표 변수가 있어 chain rule에 의한 계산은 의외로 간단하다.

저 tree를 따라 한 번에 계산하면 다음과 같다.

$$ \frac{\partial{E}}{\partial{w_{ji}}} = \frac{\partial{E}}{\partial{y_j}} \frac{\partial{y_j}}{\partial{x_j}} \frac{\partial{x_j}}{\partial{w_{ji}}} $$

 

이렇게 계산을 한 후 각 곱셈항들의 값을 차근차근 구하는 방법도 있지만, (실제로 일부 교재에서는 이렇게 내용을 전개한다.) 여기서는 논문을 바탕으로 쓰는 것이기 때문에 최대한 논문 내용을 따라 $\frac{\partial{E}}{\partial{y_j}}$, $\frac{\partial{E}}{\partial{x_j}}$, $\frac{\partial{E}}{\partial{w_{ji}}}$ 의 값들을 차근차근 구해보는 식으로 내용을 써내려가려 한다. (내겐 이런 식의 설명이 더 이해가 잘 되기도 했다.) 이런 값들을 구할 때도 여전히 chain rule을 쓰기 때문에, 위의 tree가 상당히 도움이 된다.

 

1. $\frac{\partial{E}}{\partial{y_j}}$ 구하기

$$ \frac{\partial{E}}{\partial{y_j}} = \frac{\partial{ \frac{1}{2} \sum_{j} \left( y_j - d_j \right)^2 }}{\partial{y_j}} = y_j-d_j $$

 

2. $\frac{\partial{E}}{\partial{x_j}}$ 구하기

$$ \frac{\partial{E}}{\partial{x_j}} = \frac{\partial{E}}{\partial{y_j}} \frac{\partial{y_j}}{\partial{x_j}} = \frac{\partial{E}}{\partial{y_j}} \frac{\partial{ \frac{1}{1+e^{-x_j} }}}{\partial{x_j}} = \frac{\partial{E}}{\partial{y_j}} y_j \left( 1-y_j \right) $$

마지막 등식이 성립하는 이유는, sigmoid 함수에는 다음과 같은 성질이 있기 때문이다.

$$ \sigma'(x) = \sigma(x) \left( 1-\sigma(x) \right) $$

 

여기까지 구하면, output unit의 input인 $x_j$가 error에 어떻게 영향을 미치는지 알 수 있다.

또한, (1) input $x_j$는 그 전 layer의 unit들($y_i$)로 구성된 선형 함숫값으로 볼 수 있고, (→$y_i$에 대해 편미분 가능)

동시에 (2) unit 사이에 연결된 weight($w_{ji}$)의 선형 함수 값으로 볼 수 있다. (→$w_{ji}$에 대해 편미분 가능)

우선 우리는 (2)를 먼저 사용하여, $\frac{\partial{E}}{\partial{w_{ji}}}$ 값을 구하고자 한다.

 

3. $\frac{\partial{E}}{\partial{w_{ji}}}$ 구하기

$$ \frac{\partial{E}}{\partial{w_{ji}}} = \frac{\partial{E}}{\partial{x_j}} \frac{\partial{x_j}}{\partial{w_{ji}}} = \frac{\partial{E}}{\partial{x_j}} y_i $$

마지막 등식이 성립하는 이유는 앞서 forward pass에서 언급했듯 $ x_j = \sum_{i} y_iw_{ji} $이기 때문이다.

 

이제 weight를 바꿀 때 error가 얼마나 영향을 받는지 알아냈다.

hidden layer가 없는 경우에는, 이렇게 알아낸 $\frac{\partial{E}}{\partial{w_{ji}}}$를 이용해 가중치를 갱신해주면 된다.

 

 

Back-Propagation : (2) hidden layer가 있을 때

그렇다면 중간에 hidden layer가 있는 경우에는 가중치를 어떻게 갱신할까?

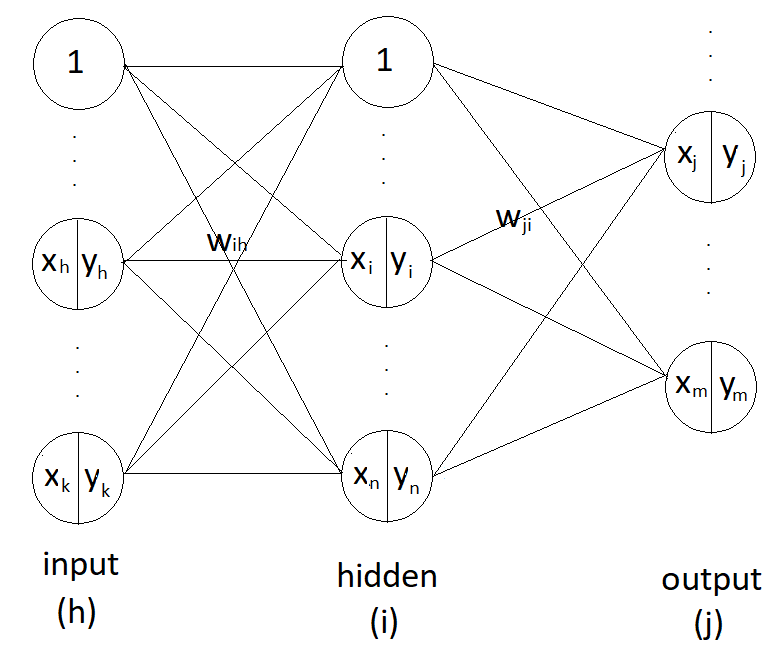
임의의 hidden layer가 하나 있는 신경망을 만들었다. input layer의 임의의 index를 h라 하자. hidden layer가 없는 신경망에서 input layer가 hidden layer로 이동했다. input layer가 새로 추가된 것 말고는 hidden layer가 없는 신경망과 동일하다.

 

아까 전 서론에서 hidden layer의 오차를 알지 못하기 때문에 가중치를 갱신하기 힘들다고 했다. 그러나 back-propagation, 오차 역전파법을 이용하면 쉽게 hidden layer의 가중치를 갱신할 수 있다.

오차 역전파법은 hidden layer의 unit의 weight들이 우리가 최종적으로 계산한 오차($E$)의 일정 부분에 관여한다는 생각에서 출발하여, 우리가 구했던 오차($E$)를 이용해 바로 전 layer 외에, 그 이전 layer들의 가중치도 갱신하는 기술이다. 오차를 역으로 전파한다는 단어의 의미 그대로다.

 

이전 unit에 대한 E의 편미분 값 ($\frac{\partial{E}}{\partial{y_i}}$)을 구하면 hidden layer가 없을 때와 동일하게 연산을 진행하여 $\frac{\partial{E}}{\partial{w_ih}}$를 구할 수 있고, 이는 hidden layer의 weight들이 오차(E)에 얼마만큼 영향을 미치는지 알 수 있음을 뜻한다. 바로 이 값을 이용해서 hidden unit들의 가중치를 갱신하는 것이다.

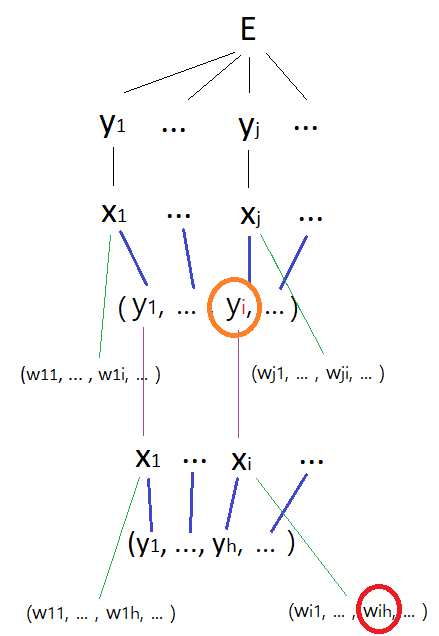
해당 신경망의 tree.

$ \frac{\partial{E}}{\partial{w_{ji}}} $ 까지는 이미 back-propagation(1)에서 구했으므로, 생략한다. 저 때 input layer라고 생각했던 것을 hidden layer라고 바꾸어 생각해주면 될 것 같다.

 

4. $\frac{\partial{E}}{\partial{y_i}}$ 구하기

가장 먼저 구해야 할 것은 $\frac{\partial{E}}{\partial{y_i}}$ 이다. (위의 tree 그림에서의 주황 동그라미) 이를 구하면 다음과 같다.

$$ \frac{\partial{E}}{\partial{y_i}} = \sum_{j} \frac{\partial{E}}{\partial{x_j}} w_{ji} $$

왜 저렇게 되는지 이해가 잘 안 될 수도 있겠으나, tree를 보면 이해가 어느 정도 될 것이다.

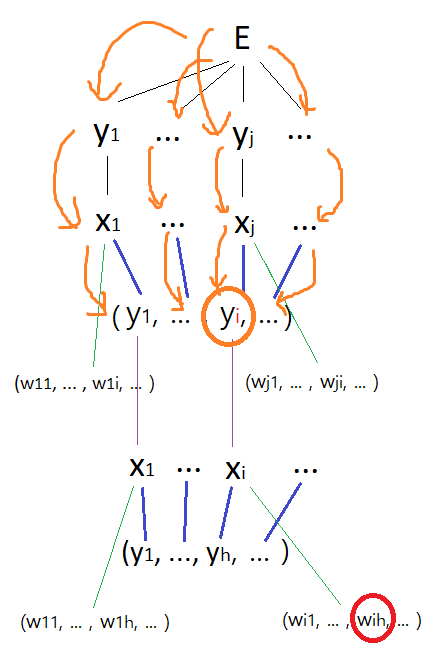
 모든 ($x_1,\ ...\ ,\ x_j,\ ...$) 들이 변수로 동일한 ($y_1,\ ...\ ,\ y_i,\ ...$)를 가지고 있으며, 위에서 언급했듯 $ x_j = \sum_{i} y_iw_{ji} $ 이기 때문이다.

 

이제 $\frac{\partial{E}}{\partial{y_i}}$를 구했으니, 아까와 동일하게 $\frac{\partial{E}}{\partial{x_i}}$, $\frac{\partial{E}}{\partial{w_{ih}}}$ 를 차례대로 구해주면 된다.

hidden layer가 하나 더 있는 경우에는, 동일하게 가중치에 대한 편미분과 더해 그 전 layer unit의 y에 대한 편미분도 함께 구해주고 계산을 똑같이 진행해주면 된다.

 

 

Optimizer

위에서 optimizer로 BGD, 그 중 momentum 기법을 사용한다고 했었다. (gradient descent에 대한 설명은 생략한다.)

자세한 식은 다음과 같다.

$$ \Delta w(t) = -\eta \frac{\partial{E}}{\partial{w(t)}} + \alpha \Delta w(t-1) $$

$\eta$는 학습률), $\alpha$는 보통 0.9의 값을 설정한다고 한다. t는 가중치가 갱신된 횟수로, epoch와 동일하게 생각하면 될 듯하다. 즉, w(t)는 이번에 갱신되는 가중치, t-1은 바로 전에 갱신되었던 가중치이다. (물론 앞에 델타가 붙으므로 변화량이다.)

위 식을 다르게 표현하면 다음과 같다.

$$ v \leftarrow\alpha  v - \eta \frac{\partial{E}}{\partial{w}} $$

$$ w \leftarrow w + v $$

 

 

번외. 논문에서 신기했던 점

출처: 참고 논문의 Fig.3

보통 요즈음 딥러닝 적용 기술하면 영상이나 자연어 처리(+음성), 추천 등이 전부인데 이 논문에서 든 예시는 조금 특이했다. 특정 가계도가 주어지고 그것을 신경망에게 학습시켜, 신경망에게 가계도의 사람 하나와 그 사람 간의 관계를 제시하면 조건에 해당하는 사람을 맞추게끔 하는 것이었다. 왜 그런가 싶었는데 이 논문의 저자 중 한 사람인 Rumelhart가 심리학자였다... 심리학 분야에서도 이런 딥러닝 기술을 연구하고 있구나 하는 게 놀라웠다. (물론 신경망 자체가 인간의 뉴런을 모방해서 만들어졌긴 하지만..) 나도 뇌과학을 잘 알지는 못하지만 뇌의 기능이나 뇌 손상으로 인한 질환 같은 분야에 흥미가 있어 책도 읽어보고 여러 영상도 봤었는데, 나중에 연구하면서 이쪽 분야와 협력하면 정말 재밌을 것 같다. (는 행복 회로였고요.... 당장 대학원 갈 생각부터 해~!!)

 

 

참고 자료

David E. Rumelhart, Geoffrey E. Hinton & Ronald J. Williams - Learning representations by back-propagating errors (1986)

우리 학교 컴퓨터 비전, 데이터 사이언스 개론 강의 자료

사이토 고키 - 밑바닥에서부터 시작하는 딥러닝

내 머릿속에 있는 미적분학 지식 by 스튜어트 sensei..